Simplifying Freedman-Lane

Posted on 19.May.2020 by A. M. Winkler

Doing a permutation test with the general linear model (GLM) in the presence of nuisance variables can be challenging. Let the model be:

$\mathbf{Y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\boldsymbol{\gamma} + \boldsymbol{\epsilon}$

where $\mathbf{Y}$ is a matrix of observed variables, $\mathbf{X}$ is a matrix of predictors of interest, $\mathbf{Z}$ is a matrix of covariates (of no interest), and $\boldsymbol{\epsilon}$ is a matrix of the same size as $\mathbf{Y}$ with the residuals.

Because the interest is in testing the relationship between $\mathbf{Y}$ and $\mathbf{X}$ , in principle it would be these that would need be permuted, but doing so also breaks the relationship with $\mathbf{Z}$ , which would be undesirable. Over the years, many methods have been proposed. A review can be found in Winkler et al. (2014); other previous work include the papers by Anderson and Legendre (1999) and Anderson and Robinson (2001).

One of these various methods is the one published in Freedman and Lane (1983), which consists of permuting data that has been residualised with respect to the covariates, then estimated covariate effects added back, then the full model fitted again. The procedure can be performed through the following steps:

Regress $\mathbf{Y}$ against the full model that contains both the effects of interest and the nuisance variables, i.e., $\mathbf{Y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\boldsymbol{\gamma} + \boldsymbol{\epsilon}$ . Use the estimated parameters $\boldsymbol{\hat{\beta}}$ to compute the statistic of interest, and call this statistic $T_{0}$ .
Regress $\mathbf{Y}$ against a reduced model that contains only the covariates, i.e. $\mathbf{Y} = \mathbf{Z}\boldsymbol{\gamma} + \boldsymbol{\epsilon}_{\mathbf{Z}}$ , obtaining estimated parameters $\boldsymbol{\hat{\gamma}}$ and estimated residuals $\boldsymbol{\hat{\epsilon}}_{\mathbf{Z}}$ .
Compute a set of permuted data $\mathbf{Y}^{*}_{j}$ . This is done by pre-multiplying the residuals from the reduced model produced in the previous step, $\boldsymbol{\hat{\epsilon}}_{\mathbf{Z}}$ , by a permutation matrix, $\mathbf{P}{j}$ , then adding back the estimated nuisance effects, i.e. $\mathbf{Y}^{*}_{j} = \mathbf{P}_{j}\boldsymbol{\hat{\epsilon}}_{\mathbf{Z}} + \mathbf{Z}\boldsymbol{\hat{\gamma}}$ .
Regress the permuted data $\mathbf{Y}^{*}_{j}$ against the full model, i.e. $\mathbf{Y}^{*}_{j} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\boldsymbol{\gamma} + \boldsymbol{\epsilon}$
Use the estimated $\boldsymbol{\hat{\beta}}^{*}_{j}$ to compute the statistic of interest. Call this statistic $T^{*}_{j}$ .
Repeat the Steps 2-4 many times to build the reference distribution of $T^{*}$ under the null hypothesis of no association between $\mathbf{Y}$ and $\mathbf{X}$ .
Count how many times $T^{*}_{j}$ was found to be equal to or larger than $T_{0}$ , and divide the count by the number of permutations; the result is the p-value.

Steps 1-4 can be written concisely as:

$\left(\mathbf{P}_{j}\mathbf{R}_{\mathbf{Z}}+\mathbf{H}_{\mathbf{Z}}\right) \mathbf{Y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\boldsymbol{\gamma}+\boldsymbol{\epsilon}$

where $\mathbf{P}_{j}$ is a permutation matrix (for the $j$ -th permutation, $\mathbf{H}_{\mathbf{Z}}=\mathbf{Z}\mathbf{Z}^{+}$ is the hat matrix due to the covariates, and $\mathbf{R}_{\mathbf{Z}} = \mathbf{I} - \mathbf{H}_{\mathbf{Z}}$ is the residual forming matrix; the superscript symbol $^{+}$ represents a matrix pseudo-inverse.

In page 385 of Winkler et al. (2014), my colleagues and I state that:

[…] add the nuisance variables back in Step 3 is not strictly necessary, and the model can be expressed simply as $\mathbf{P}_{j}\mathbf{R}_{\mathbf{Z}}\mathbf{Y}=\mathbf{X}\boldsymbol{\beta}+\mathbf{Z}\boldsymbol{\gamma}+\boldsymbol{\epsilon}$ , implying that the permutations can actually be performed just by permuting the rows of the residual-forming matrix $\mathbf{R}_{\mathbf{Z}}$ .

However, in the paper we do not offer any proof of this important result, that allows algorithmic acceleration. Here we remedy that. Let’s start with two brief lemmata:

Lemma 1: The product of a hat matrix and its corresponding residual-forming matrix is zero, that is, $\mathbf{R}_{\mathbf{Z}}\mathbf{H}_{\mathbf{Z}} = \mathbf{H}_{\mathbf{Z}}\mathbf{R}_{\mathbf{Z}} = \mathbf{0}$ .

This is because $\mathbf{R}_{\mathbf{Z}} = \mathbf{I} - \mathbf{H}_{\mathbf{Z}}$ , hence $\mathbf{R}_{\mathbf{Z}}\mathbf{H}_{\mathbf{Z}} = \mathbf{R}_{\mathbf{Z}}(\mathbf{I} - \mathbf{R}_{\mathbf{Z}}) = \mathbf{R}_{\mathbf{Z}} - \mathbf{R}_{\mathbf{Z}}\mathbf{R}_{\mathbf{Z}} = \mathbf{R}_{\mathbf{Z}} - \mathbf{R}_{\mathbf{Z}} = \mathbf{0}$ since $\mathbf{R}_{\mathbf{Z}}$ is idempotent.

Lemma 2 (Frisch–Waugh–Lovell theorem): Given a GLM expressed as $\mathbf{Y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\boldsymbol{\gamma} + \boldsymbol{\epsilon}$ , we can estimate $\boldsymbol{\beta}$ from an equivalent GLM written as $\mathbf{R}_{\mathbf{Z}}\mathbf{Y} = \mathbf{R}_{\mathbf{Z}}\mathbf{X}\boldsymbol{\beta} + \mathbf{R}_{\mathbf{Z}}\boldsymbol{\epsilon}$ .

To see why, remember that multiplying both sides of an equation by the same factor does not change it (least squares solutions may change; transformations using Lemma 2 below do not act on the fitted model). Let’s start from:

$\mathbf{R}_{\mathbf{Z}}\mathbf{Y} = \mathbf{R}_{\mathbf{Z}}(\mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\boldsymbol{\gamma} + \boldsymbol{\epsilon})$

Then remove the parentheses:

$\mathbf{R}_{\mathbf{Z}}\mathbf{Y} = \mathbf{R}_{\mathbf{Z}}\mathbf{X}\boldsymbol{\beta} + \mathbf{R}_{\mathbf{Z}}\mathbf{Z}\boldsymbol{\gamma} + \mathbf{R}_{\mathbf{Z}}\boldsymbol{\epsilon}$

Since $\mathbf{R}_{\mathbf{Z}} = \mathbf{I} - \mathbf{H}_{\mathbf{Z}}$ :

$\mathbf{R}_{\mathbf{Z}}\mathbf{Y} = \mathbf{R}_{\mathbf{Z}}\mathbf{X}\boldsymbol{\beta} + (\mathbf{I}-\mathbf{H}_{\mathbf{Z}})\mathbf{Z}\boldsymbol{\gamma} + \mathbf{R}_{\mathbf{Z}}\boldsymbol{\epsilon}$

and that $\mathbf{H}_{\mathbf{Z}} = \mathbf{Z}\mathbf{Z}^{+}$ :

$\mathbf{R}_{\mathbf{Z}}\mathbf{Y} = \mathbf{R}_{\mathbf{Z}}\mathbf{X}\boldsymbol{\beta} + (\mathbf{Z}-\mathbf{Z}\mathbf{Z}^{+}\mathbf{Z})\boldsymbol{\gamma} + \mathbf{R}_{\mathbf{Z}}\boldsymbol{\epsilon}$

Since $\mathbf{Z}^{+}\mathbf{Z}=\mathbf{I}$ :

$\mathbf{R}_{\mathbf{Z}}\mathbf{Y} = \mathbf{R}_{\mathbf{Z}}\mathbf{X}\boldsymbol{\beta} + \mathbf{0}\boldsymbol{\gamma} + \mathbf{R}_{\mathbf{Z}}\boldsymbol{\epsilon}$

$\mathbf{R}_{\mathbf{Z}}\mathbf{Y} = \mathbf{R}_{\mathbf{Z}}\mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon}_{\mathbf{Z}}$

where $\boldsymbol{\epsilon}_{\mathbf{Z}}= \mathbf{R}_{\mathbf{Z}}\boldsymbol{\epsilon}$ .

Main result

Now we are ready for the main result. The Freedman-Lane model is:

$\left(\mathbf{P}_{j}\mathbf{R}_{\mathbf{Z}}+\mathbf{H}_{\mathbf{Z}}\right) \mathbf{Y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\boldsymbol{\gamma}+\boldsymbol{\epsilon}$

Per Lemma 2, it can be rewritten as:

$\mathbf{R}_{\mathbf{Z}}\left(\mathbf{P}_{j}\mathbf{R}_{\mathbf{Z}}+\mathbf{H}_{\mathbf{Z}}\right) \mathbf{Y} = \mathbf{R}_{\mathbf{Z}}\mathbf{X}\boldsymbol{\beta}+\boldsymbol{\epsilon}_{\mathbf{Z}}$

Dropping the parenthesis:

$\mathbf{R}_{\mathbf{Z}}\mathbf{P}_{j}\mathbf{R}_{\mathbf{Z}}\mathbf{Y} +\mathbf{R}_{\mathbf{Z}}\mathbf{H}_{\mathbf{Z}} \mathbf{Y} = \mathbf{R}_{\mathbf{Z}}\mathbf{X}\boldsymbol{\beta}+\boldsymbol{\epsilon}_{\mathbf{Z}}$

Per Lemma 1:

$\mathbf{R}_{\mathbf{Z}}\mathbf{P}_{j}\mathbf{R}_{\mathbf{Z}}\mathbf{Y} + \mathbf{0}\mathbf{Y} = \mathbf{R}_{\mathbf{Z}}\mathbf{X}\boldsymbol{\beta}+\boldsymbol{\epsilon}_{\mathbf{Z}}$

$\mathbf{R}_{\mathbf{Z}}\mathbf{P}_{j}\mathbf{R}_{\mathbf{Z}}\mathbf{Y}= \mathbf{R}_{\mathbf{Z}}\mathbf{X}\boldsymbol{\beta}+\boldsymbol{\epsilon}_{\mathbf{Z}}$

What is left has the same form as the result of Lemma 2. Thus, reversing it, we obtain the final result:

$\mathbf{P}_{j}\mathbf{R}_{\mathbf{Z}} \mathbf{Y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Z}\boldsymbol{\gamma} +\boldsymbol{\epsilon}$

Hence, the hat matrix $\mathbf{H}_{\mathbf{Z}}$ cancels out, meaning that it is not necessary. Results are the same both ways.

References

Anderson MJ, Legendre P. An empirical comparison of permutation methods for tests of partial regression coefficients in a linear model. Journal of Statistical Computation and Simulation 1999;62(3):271–303.
Anderson MJ, Robinson J. Permutation tests for linear models. Australian & New Zealand Journal of Statistics of Statistics 2001;43(1):75–88.
Freedman D, Lane D. A Nonstochastic Interpretation of Reported Significance Levels. Journal of Business & Economic Statistics 1983;1(4):292.
Winkler AM, Ridgway GR, Webster MA, Smith SM, Nichols TE. Permutation inference for the general linear model. NeuroImage 2014;92:381–97.

Updates

07.Jun.2020: A graphical representation of Lemma 1 can be found in p.40 of Jaromil Frossard PhD thesis (Université de Genève), available here.
07.Jun.2020: Lemma 2 corresponds to the Frisch–Waugh–Lovell theorem. Thanks to Samuel Davenport (University of Oxford) for pointing out.

Better statistics, faster

Posted on 09.August.2016 by A. M. Winkler

Faster permutation inference

Permutation tests are more robust and help to make scientific results more reproducible by depending on fewer assumptions. However, they are computationally intensive as recomputing a model thousands of times can be slow. The purpose of this post is to briefly list some options available for speeding up permutation.

Firstly, no speed-ups may be needed: for small sample sizes, or low resolutions, or small regions of interest, a permutation test can run in a matter of minutes. For larger data, however, accelerations may be of use. One option is acceleration through parallel processing or GPUs (for example applications of the latter, see Eklund et al., 2012, Eklund et al., 2013 and Hernández et al., 2013; references below), though this does require specialised implementation. Another option is to reduce the computational burden by exploiting the properties of the statistics and their distributions. A menu of options includes:

Do few permutations (shorthand name: fewperms). The results remain valid on average, although the p-values will have higher variability.
Keep permuting until a fixed number of permutations with statistic larger than the unpermuted is found (a.k.a., negative binomial; shorthand name: negbin).
Do a few permutations, then approximate the tail of the permutation distribution by fitting a generalised Pareto distribution to its tail (shorthand name: tail).
Approximate the permutation distribution with a gamma distribution, using simple properties of the test statistic itself, amazingly not requiring any permutations at all (shorthand name: noperm).
Do a few permutations, then approximate the full permutation distribution by fitting a gamma distribution (shorthand name: gamma).
Run permutations on only a few voxels, then fill the missing ones using low-rank matrix completion theory (shorthand name: lowrank).

These strategies allow accelerations >100x, yielding nearly identical results as in the non-accelerated case. Some, such as tail approximation, are generic enough to be used nearly all the most common scenarios, including univariate and multivariate tests, spatial statistics, and for correction for multiple testing.

In addition to accelerating permutation tests, some of these strategies, such as tail and noperm, allow continuous p-values to be found, and refine the p-values far into the tail of the distribution, thus avoiding the usual discreteness of p-values, which can be a problem in some applications if too few permutations are done.

These methods are available in the tool PALM — Permutation Analysis of Linear Models — and the complete description, evaluation, and application to the re-analysis of a voxel-based morphometry study (Douaud et al., 2007) have been just published in Winkler et al., 2016 (for the Supplementary Material, click here). The paper includes a flow chart prescribing these various approaches for each case, reproduced below.

The hope is that these accelerations will facilitate the use of permutation tests and, if used in combination with hardware and/or software improvements, can further expedite computation leaving little reason not to use these tests.

References

Douaud G, Smith S, Jenkinson M, Behrens T, Johansen-Berg H, Vickers J, James S, Voets N, Watkins K, Matthews PM, James A. Anatomically related grey and white matter abnormalities in adolescent-onset schizophrenia. Brain. 2007 Sep;130(Pt 9):2375-86. Epub 2007 Aug 13.
Eklund A, Andersson M, Knutsson H. fMRI analysis on the GPU-possibilities and challenges. Comput Methods Programs Biomed. 2012 Feb;105(2):145-61.
Eklund A, Dufort P, Forsberg D, LaConte SM. Medical image processing on the GPU – Past, present and future. Med Image Anal. 2013;17(8):1073-94.
Hernández M, Guerrero GD, Cecilia JM, García JM, Inuggi A, Jbabdi S, et al. Accelerating fibre orientation estimation from diffusion weighted magnetic resonance imaging using GPUs. PLoS One. 2013 Jan;8(4):e61892.1.
Winkler AM, Ridgway GR, Webster MA, Smith SM, Nichols TE. Permutation inference for the general linear model. Neuroimage. 2014 May 15;92:381-97.
Winkler AM, Ridgway GR, Douaud G, Nichols TE, Smith SM. Faster permutation inference in brain imaging. Neuroimage. 2016 Jun 7;141:502-516.

Contributed to this post: Tom Nichols, Ged Ridgway.

Three HCP utilities

Posted on 01.August.2016 by A. M. Winkler

If you are working with data from the Human Connectome Project (HCP), perhaps these three small Octave/MATLAB utilities may be of some use:

hcp2blocks.m: Takes the restricted file with information about kinship and zygosity and produces a multi-level exchangeability blocks file that can be used with PALM for permutation inference. It is fully described here.
hcp2solar.m: Takes restricted and unrestricted files to produce a pedigree file that can be used with SOLAR for heritability and genome-wide association analyses.
picktraits.m: Takes either restricted or unrestricted files, a list of traits and a list of subject IDs to produce tables with selected traits for the selected subjects. These can be used to, e.g., produce design matrices for subsequent analysis.

These functions need to parse relatively large CSV files, which is somewhat inefficient in MATLAB and Octave. Still, since these commands usually have to be executed only once for a particular analysis, a 1-2 minute wait seems acceptable.

If downloaded directly from the above links, remember also to download the prerequisites: strcsvread.m and strcsvwrite.m. Alternatively, clone the full repository from GitHub. The link is this. Other tools may be added in the future.

A fourth utility

For the HCP-S1200 release (March/2017), zygosity information is provided in the fields ZygositySR (self-reported zygosity) and ZygosityGT (zygosity determined by genetic methods for select subjects). If needed, these two fields can be merged into a new field named simply Zygosity. To do so, use a fourth utility, command mergezyg.

Extreme value notes

Posted on 01.March.2016 by A. M. Winkler

Extreme values are useful to quantify the risk of catastrophic floods, and much more.

This is a brief set of notes with an introduction to extreme value theory. For reviews, see Leadbetter et al (1983) and David and Huser (2015) [references at the end]. Also of some (historical) interest might be the classical book by Gumbel (1958). Let $X_1, \dots, X_n$ be a sequence of independent and identically distributed variables with cumulative distribution function (cdf) $F(x)$ and let $M_n =\max(X_1,\dots,X_n)$ denote the maximum.

If $F(x)$ is known, the distribution of the maximum is:

$\begin{array}{lll} P(M_n \leqslant x) &=&P(X_1 \leqslant x, \dots, X_n \leqslant x) \\ &=& P(X_1 \leqslant x) \cdots P(X_n \leqslant x) = F^n(x). \end{array}$

The distribution function $F(x)$ might, however, not be known. If data are available, it can be estimated, although small errors on the estimation of $F(x)$ can lead to large errors concerning the extreme values. Instead, an asymptotic result is given by the extremal types theorem, also known as Fisher-Tippett-Gnedenko Theorem, First Theorem of Extreme Values, or extreme value trinity theorem (called under the last name by Picklands III, 1975).

But before that, let’s make a small variable change. Working with $M_n$ directly is problematic because as $n \rightarrow \infty$ , $F^n(x) \rightarrow 0$ . Redefining the problem as a function of $M_n^* = \frac{M_n-b_n}{a_n}$ renders treatment simpler. The theorem can be stated then as: If there exist sequences of constants $a_n \in \mathbb{R}_{+}$ and $b_n \in \mathbb{R}$ such that, as $n \rightarrow \infty$ :

$P\left(M_{n}^{*} \leqslant x \right) \rightarrow G(x)$

then $G(x)$ belongs to one of three “domains of attraction”:

Type I (Gumbel law): $\Lambda(x) = e^{-e^{-\frac{x-b}{a}}}$ , for $x \in \mathbb{R}$ indicating that the distribution of $M_n$ has an exponential tail.
Type II (Fréchet law): $\Phi(x) = \begin{cases} 0 & x\leqslant b \\ e^{-\left(\frac{x-b}{a}\right)^{-\alpha}} & x\; \textgreater\; b \end{cases}$ indicating that the distribution of $M_n$ has a heavy tail (including polynomial decay).
Type III (Weibull law): $\Psi(x) = \begin{cases} e^{-\left( -\frac{x-b}{a}\right)^\alpha} & x\;\textless\; b \\ 1 & x\geqslant b \end{cases}$ indicating that the distribution of $M_n$ has a light tail with finite upper bound.

Note that in the above formulation, the Weibull is reversed so that the distribution has an upper bound, as opposed to a lower one as in the Weibull distribution. Also, the parameterisation is slightly different than the one usually adopted for the Weibull distribution.

These three families have parameters $a\; \textgreater\; 0$ , $b$ and, for families II and III, $\alpha\; \textgreater\; 0$ . To which of the three a particular $F(x)$ is attracted is determined by the behaviour of the tail of of the distribution for large $x$ . Thus, we can infer about the asymptotic properties of the maximum while having only a limited knowledge of the properties of $F(x)$ .

These three limiting cases are collectively termed extreme value distributions. Types II and III were identified by Fréchet (1927), whereas type I was found by Fisher and Tippett (1928). In his work, Fréchet used $M_n^* = \frac{M_n}{a_n}$ , whereas Fisher and Tippett used $M_n^* = \frac{M_n-b_n}{a_n}$ . Von Mises (1936) identified various sufficient conditions for convergence to each of these forms, and Gnedenko (1943) established a complete generalisation.

Generalised extreme value distribution

As shown above, the rescaled maxima converge in distribution to one of three families. However, all are cases of a single family that can be represented as:

$G(x) = e^{-\left(1-\xi\left(\frac{x-\mu}{\sigma}\right)\right)^{\frac{1}{\xi}}}$

defined on the set $\left\{x:1-\xi\frac{x-\mu}{\sigma}\;\textgreater\;0\right\}$ , with parameters $-\infty \;\textless \;\mu\;\textless\; \infty$ (location), $\sigma\;\textgreater\;0$ (scale), and $-\infty\;\textless\;\xi\;\textless\;\infty$ (shape). This is the generalised extreme value (GEV) family of distributions. If $\xi \rightarrow 0$ , it converges to Gumbel (type I), whereas if $\xi < 0$ it corresponds to Fréchet (type II), and if $\xi\;\textgreater\;0$ it corresponds to Weibull (type III). Inference on $\xi$ allows choice of a particular family for a given problem.

Generalised Pareto distribution

For $u\rightarrow\infty$ , the limiting distribution of a random variable $Y=X-u$ , conditional on $X \;\textgreater\; u$ , is:

$H(y) = 1-\left(1-\frac{\xi y}{\tilde{\sigma}}\right)^{\frac{1}{\xi}}$

defined for $y \;\textgreater\; 0$ and $\left(1-\frac{\xi y}{\tilde{\sigma}}\right) \;\textgreater\; 0$ . The two parameters are the $\xi$ (shape) and $\tilde{\sigma}$ (scale). The shape corresponds to the same parameter $\xi$ of the GEV, whereas the scale relates to the scale of the former as $\tilde{\sigma}=\sigma-\xi(u-\mu)$ .

The above is sometimes called the Picklands-Baikema-de Haan theorem or the Second Theorem of Extreme Values, and it defines another family of distributions, known as generalised Pareto distribution (GPD). It generalises an exponential distribution with parameter $\frac{1}{\tilde{\sigma}}$ as $\xi \rightarrow 0$ , an uniform distribution in the interval $\left[0, \tilde{\sigma}\right]$ when $\xi = 1$ , and a Pareto distribution when $\xi \;\textgreater\; 0$ .

Parameter estimation

By restricting the attention to the most common case of $-\frac{1}{2}<\xi<\frac{1}{2}$ , which represent distributions approximately exponential, parametters for the GPD can be estimated using at least three methods: maximum likelihood, moments, and probability-weighted moments. These are described in Hosking and Wallis (1987). For $\xi$ outside this interval, methods have been discussed elsewhere (Oliveira, 1984). The method of moments is probably the simplest, fastest and, according to Hosking and Wallis (1987) and Knijnenburg et al (2009), has good performance for the typical cases of $-\frac{1}{2}<\xi<\frac{1}{2}$ .

For a set of extreme observations, let $\bar{x}$ and $s^2$ be respectively the sample mean and variance. The moment estimators of $\tilde{\sigma}$ and $\xi$ are $\hat{\tilde{\sigma}} = \frac{\bar{x}}{2}\left(\frac{\bar{x}^2}{s^2}+1\right)$ and $\hat{\xi}=\frac{1}{2}\left(\frac{\bar{x}^2}{s^2}-1\right)$ .

The accuracy of these estimates can be tested with, e.g., the Anderson-Darling goodness-of-fit test (Anderson and Darling, 1952; Choulakian and Stephens, 2001), based on the fact that, if the modelling is accurate, the p-values for the distribution should be uniformly distributed.

Availability

Statistics of extremes are used in PALM as a way to accelerate permutation tests. More details to follow soon.

References

Anderson TW, Darling DA. Asymptotic theory of certain goodness of fit criteria based on stochastic processes. Ann Math Stat. 1952;23(2):193-212.
Choulakian V, Stephens MA. Goodness-of-Fit Tests for the Generalized Pareto Distribution. Technometrics. 2001;43(4):478-84.
Davison AC, Huser R. Statistics of Extremes. Annu Rev Stat Its Appl. 2015;2(1):203-35.
Fisher RA, Tippett LHC. Limiting forms of the frequency distribution of the largest and smallest member of a sample. Proc Camb Philol Soc. 1928;24:180-90.
Fréchet, M. Sur la loi de probabilité de l’écart maximum. Ann Soc Polon Math. 1927;6:93. [link currently not accessible due to copyright issues]
Gnedenko B. Sur La Distribution Limite Du Terme Maximum D’Une Serie Aleatoire. Ann Math. 1943;44(3):423-53.
Gumbel E. Statistics of Extremes. Echo Point Books & Media, 1958.
Hosking JRM, Wallis JR. Parameter and quantile estimation for the generalized Pareto distribution. Technometrics. 1987;29:339-49.
Knijnenburg TA, Wessels LFA, Reinders MJT, Shmulevich I. Fewer permutations, more accurate P-values. Bioinformatics. 2009 Jun 15;25(12):i161-8.
Leadbetter MR, Lindgren G, Rootzén H. Extremes and related properties of
random sequences and processes. Springer-Verlag, New York, 1983.
Oliveira JT (ed). Proceedings of the NATO Advanced Study Institute on Statistical Extremes and Applications. D. Heidel, Dordrecht, Holland, 1984.
Picklands III J. Statistical inference using extreme order statistics. Ann Stat. 1975;3(1):119-31.
Tippett LHC. On the extreme individuals and the range of samples taken from a normal population. Biometrika. 1925;17(3):364-87.
von Mises R. La distribution de la plus grande de n valeurs. Rev Mathématique l’Union Interbalkanique. 1936;1:141-60.

The figure at the top (flood) is in public domain.

Non-Parametric Combination (NPC) for brain imaging

Posted on 08.February.2016 by A. M. Winkler

Have you ever had an analysis in which there was a large set of contrasts, all of interest, and you were worried about multiple testing? An eventual effect would be missed by a simple Bonferroni correction, but you did not know what else to do? Or did you have a set of different studies and you wished to obtain a style of meta-analytic result, indicating whether there would be evidence across all of them, without requiring the studies to be all consistently significant?

The Non-Parametric Combination (NPC) solves these issues. It is a way of performing joint inference on multiple data collected on the same experimental units (e.g., same subjects), all with minimal assumptions. The method was proposed originally by Pesarin (1990, 1992) [see references below], independently by Blair and Karninski (1993), and described extensively by Pesarin and Salmaso (2010). In this blog entry, the NPC is presented in brief, with emphasis on the modifications we introduce to render it feasible for brain imaging. The complete details are in our paper that has just been published in the journal Human Brain Mapping.

NPC in a nutshell

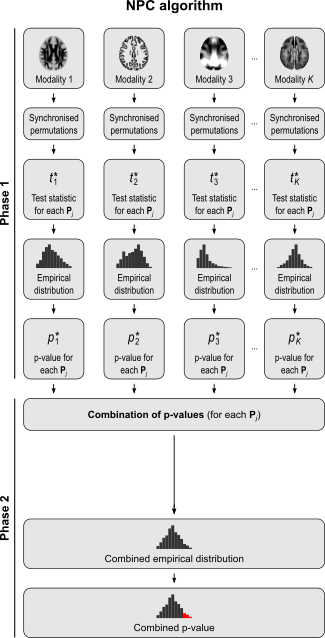
The NPC consists of, in a first phase, testing each hypothesis separately using permutations that are performed synchronously across datasets; these tests are termed partial tests. The resulting statistics for each and every permutation are recorded, allowing an estimate of the complete empirical null distribution to be constructed for each one. In a second phase, the empirical p-values for each statistic are combined, for each permutation, into a joint statistic. As such a combined joint statistic is produced from the previous permutations, an estimate of its empirical distribution function is immediately known, and so is the p-value of the joint test. A flowchart of the original algorithm is shown below; click to see it side-by-side with the modified one (described below).

A host of combining functions

The null hypothesis of the NPC is that null hypotheses for all partial tests are true, and the alternative hypothesis that any is false, which is the same null of a union-intersection test (UIT; Roy, 1953). The rejection region depends on how the combined statistic is produced. Various combining functions, which produce such combined statistics, can be considered, and some of the most well known are listed in the table below:

Method	Statistic	p-value
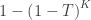Tippett	$\min \left(p_{k}\right)$	$1-\left(1-T\right)^{K}$
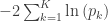Fisher	$-2 \sum_{k=1}^{K} \ln\left(p_{k}\right)$	$1-\chi^{2}\left(T;\;\nu=2K\right)$
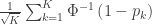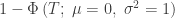Stouffer	$\frac{1}{\sqrt{K}} \sum_{k=1}^{K} \Phi^{-1}\left(1-p_{k}\right)$	$1-\Phi\left(T;\;\mu=0,\;\sigma^2=1\right)$
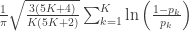Mudholkar–George	$\frac{1}{\pi}\sqrt{\frac{3(5K+4)}{K(5K+2)}}\sum_{k=1}^{K} \ln\left(\frac{1-p_{k}}{p_{k}}\right)$	$1-t_{\text{cdf}}(T;\;\nu=5K+4)$

In the table, $K$ is the number of partial tests, and the remaining of the variables follow the usual notation (see the Table 1 in the paper for the complete description). Many of these combining functions were proposed over the years for applications such as meta-analyses, and many of them assume independence between the tests being combined, and will give incorrect p-values if such assumption is not met. In the NPC, lack of dependence is not a problem, even if these same functions are used: the synchronised permutations ensure that any dependence, if existing, is taken into account, and this is done so implicitly, with no need for explicit modelling.

The different combining functions lead to different rejection regions for the null hypothesis. For the four combining functions in the table above, the respective rejection regions are in the figure below.

The combining functions can be modified to allow combination of tests so as to favour hypotheses with concordant directions, or be modified for bi-directional tests. Click on the figure above for examples of these cases (again, see the paper for the complete details).

Two problems, one solution

The multiple testing problem is well known in brain imaging: as an image comprises thousands of voxels/vertices/faces, correction is necessary. Bonferroni is in general too conservative, and various other approaches have been proposed, such as the random field theory. Permutation tests provide control over the familywise error rate (FWER) for the multiple tests across space, requiring only the assumption of exchangeability. This is all well known; see Nichols and Hayasaka (2003) and Winkler et al. (2014) for details.

However, another type of multiple testing is also common: analyses that test multiple hypotheses using the same model, multiple pairwise group comparisons, multiple and distinct models, studies using multiple modalities, that mix imaging and non-imaging data, that consider multiple processing pipelines, and even multiple multivariate analyses. All these common cases also need multiple testing correction. We call this multiple testing problem MTP-II, to discern it from the well known multiple testing problem across space, described above, which we term MTP-I.

One of the many combining functions possible with NPC, the one proposed by Tippett (1931), has a further property that makes it remarkably interesting. The Tippett function uses the smallest p-value across partial tests as its test statistic. Alternatively, if all statistics are comparable, it can be formulated in terms of the maximum statistic. It turns out that the distribution of the maximum statistic across a set of tests is also the distribution that can be used in a closed testing procedure (Marcus et al., 1976) to correct for the familywise error rate (FWER) using resampling methods, such as permutation. In the context of joint inference, FWER-correction can also be seen as an UIT. Thus, NPC offers a link between combination of multiple tests, and correction for multiple tests, in both cases regardless of any dependence between such tests.

This means that the MTP-II, for which correction in the parametric realm is either non-existing or fiendishly difficult, can be accommodated easily. It requires no explicit modelling of the dependence between the tests, and the resulting error rates are controlled exactly at the test level, adding rigour to what otherwise could lead to an excess of false positives without correction, or be overly conservative if a naïve correction such as Bonferroni were attempted.

Modifying for imaging applications

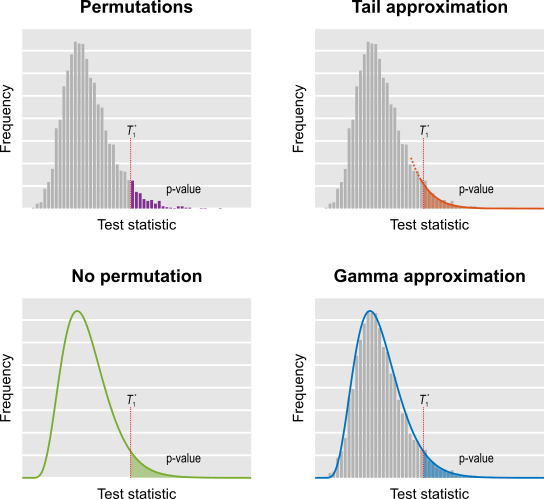
As originally proposed, in practice NPC cannot be used in brain imaging. As the statistics for all partial tests for all permutations need to be recorded, an enormous amount of space for data storage is necessary. Even if storage space were not a problem, the discreteness of the p-values for the partial tests is problematic when correcting for multiple testing, because with thousands of tests in an image, ties are likely to occur, further causing ties among the combined statistics. If too many tests across an image share the same most extreme statistic, correction for the MTP-I, while still valid, becomes less powerful (Westfall and Young, 1993; Pantazis et al., 2005). The most obvious workaround — run an ever larger number of permutations to break the ties — may not be possible for small sample sizes, or when possible, requires correspondingly larger data storage.

The solution is loosely based on the direct combination of the test statistics, by converting the test statistics of the partial tests to values that behave as p-values, using the asymptotic distribution of the statistics for the partial tests. We call these as “u-values”, in order to emphasise that they are not meant to be read or interpreted as p-values, but rather as transitional values that allow combinations that otherwise would not be possible.

For spatial statistics, the asymptotic distribution of the combined statistic is used, this time to produce a z-score, which can be subjected to the computation of cluster extent, cluster mass, and/or threshold-free cluster enhancement (TFCE; Smith and Nichols, 2009). A flow chart of the modified algorithm is shown below. Click to see it side-by-side with the original.

More power, fewer assumptions

One of the most remarkable features of NPC is that the synchronised permutations implicitly account for the dependence structure among the partial tests. This means that even combining methods originally derived under the assumption of independence can be used when such independence is untenable. As the p-values are assessed via permutations, distributional restrictions are likewise not necessary, liberating NPC from most assumptions that thwart parametric methods in general. This renders NPC a good alternative to classical multivariate tests, such as MANOVA, MANCOVA, and Hotelling’s T² tests: each of the response variables can be seen as an univariate partial test in the context of the combination, but without the assumptions that are embodied in these old multivariate tests.

As if all the above were not already sufficient, NPC is also more powerful than such classical multivariate tests. This refers to its finite sample consistency property, that is, even with fixed sample size, as the number of modalities being combined increases, the power of the test also increases. The power of classical multivariate tests, however, increases up to a certain point, then begins to decrease, eventually reaching zero when the number of combining variables match the sample size.

The figure below summarises the analysis of a subset of the subjects of a published FMRI study (Brooks et al, 2005) in which painful stimulation was applied to the face, hand, and foot of 12 subjects. Using permutation tests separately, no results could be identified for any of the three types of stimulation. A simple multivariate test, the Hotelling’s T² test, even assessed using permutations, did not reveal any effect of stimulation either. The NPC results, however, suggest involvement of large portions of the anterior insula and secondary somatosensory cortex. The Fisher, Stouffer and Mudholkar–George combining functions were particularly successful in recovering a small area of activity in the midbrain and periaqueductal gray area, which would be expected from previous studies on pain, but that could not be located from the original, non-combined data.

Detailed assessment of power, using variable number of modalities, and of modalities containing signal, is shown in the paper.

Combinations or conjunctions?

Combination, as done via NPC, is different than conjunctions (Nichols et al., 2005) in the following: in the combination, one seeks for aggregate significance across partial tests, without the need that any individual study is necessarily significant. In the conjunction, it is necessary that all of them, with no exception, is significant. As indicated above, the NPC forms an union-intersection test (UIT; Roy, 1953), whereas the conjunctions form an intersection-union test (IUT; Berger, 1982). The former can be said to be significant if any (or an aggregate) of the partial tests is significant, whereas the latter is significant if all the partial tests are.

Availability

The NPC, with the modifications for brain imaging, is available in the tool PALM — Permutation Analysis of Linear Models. It runs in either Matlab or Octave, and is free (GPL).

References

Berger RL. Multiparameter hypothesis testing and acceptance sampling. Technometrics. 1982;24(4):295-300.
Blair RC, Karniski W. An alternative method for significance testing of waveform difference potentials. Psychophysiology. 1993;30(5):518-24.
Brooks JCW, Zambreanu L, Godinez A, Craig ADB, Tracey I. Somatotopic organisation of the human insula to painful heat studied with high resolution functional imaging. Neuroimage. 2005;27(1):201-9.
Nichols T, Brett M, Andersson J, Wager T, Poline J-B. Valid conjunction inference with the minimum statistic. Neuroimage. 2005 Apr 15;25(3):653-60.
Nichols T, Hayasaka S. Controlling the familywise error rate in functional neuroimaging: a comparative review. Stat Methods Med Res. 2003 Oct;12(5):419-46.
Pantazis D, Nichols TE, Baillet S, Leahy RM. A comparison of random field theory and permutation methods for the statistical analysis of MEG data. Neuroimage. 2005;25(2):383-94.
Pesarin F. On a nonparametric combination method for dependent permutation tests with applications. Psychother Psychosom. 1990;54:172-9.
Pesarin F. A resampling procedure for nonparametric combination of several dependent tests. J Ital Stat Soc. 1992;1(1):87-101.
Pesarin F, Salmaso L. Permutation Tests for Complex Data: Theory, Applications and Software. John Wiley and Sons, West Sussex, England, UK, 2010.
Roy SN. On a Heuristic Method of Test Construction and its use in Multivariate Analysis. Ann Math Stat. 1953 Jun;24(2):220-38.
Smith SM, Nichols TE. Threshold-free cluster enhancement: addressing problems of smoothing, threshold dependence and localisation in cluster inference. Neuroimage. 2009;44(1):83-98.
Tippett LHC. The methods of statistics. Williams and Northgate, London, 1931.
Westfall PH, Young SS. Resampling-Based Multiple Testing: Examples and Methods for p-Value Adjustment. John Wiley and Sons, New York, 1993.
Winkler AM, Ridgway GR, Webster MA, Smith SM, Nichols TE. Permutation inference for the general linear model. Neuroimage. 2014;92:381-97 (Open Access).
Winkler AM, Webster MA, Brooks JC, Tracey I, Smith SM, Nichols TE. Non-parametric combination and related permutation tests for neuroimaging. Hum Brain Mapp. 2016 Feb 5 (in press, Open Access). The Supporting Information can be browsed directly here. This paper supersedes our earlier poster presented in the 2013 OHBM conference.

Contributed to this post: Tom Nichols.

Permutation tests in the Human Connectome Project

Posted on 07.December.2015 by A. M. Winkler

Permutation tests are known to be superior to parametric tests: they are based on only few assumptions, essentially that the data are exchangeable, and allow the correction for the multiplicity of tests and the use of various non-standard statistics. The exchangeability assumption allows data to be permuted whenever their joint distribution remains unaltered. Usually this means that each observation needs to be independent from the others.

In many studies, however, there are repeated measurements on the same subjects, which violates exchangeability: clearly, the various measurements obtained from a given subject are not independent from each other. In the Human Connectome Project (HCP) (Van Essen et al, 2012; 2013; see references at the end), subjects are sampled along with their siblings (most of them are twins), such that independence cannot be guaranteed either.

In Winkler et al. (2014), certain structured types of non-independence in brain imaging were addressed through the definition of exchangeability blocks (EBs). Observations within EB can be shuffled freely or, alternatively, the EBs themselves can be shuffled as a whole. This allows various designs that otherwise could not be assessed through permutations.

The same idea can be generalised for blocks that are nested within other blocks, in a multi-level fashion. In the paper Multi-level Block Permutation (Winkler et al., 2015) we presented a method that allows blocks to be shuffled a whole, and inside them, sub-blocks are further allowed to be shuffled, in a recursive process. The method is flexible enough to accommodate permutations, sign-flippings (sometimes also called “wild bootstrap”), and permutations together with sign-flippings.

In particular, this permutation scheme allows the data of the HCP to be analysed via permutations: subjects are allowed to be shuffled with their siblings while keeping the joint distribution intra-sibship maintained. Then each sibship is allowed to be shuffled with others of the same type.

In the paper we show that the error type I is controlled at the nominal level, and the power is just marginally smaller than that would be obtained by permuting freely if free permutation were allowed. The more complex the block structure, the larger the reductions in power, although with large sample sizes, the difference is barely noticeable.

Importantly, simply ignoring family structure in designs as this causes the error rates not to be controlled, with excess false positives, and invalid results. We show in the paper examples of false positives that can arise, even after correction for multiple testing, when testing associations between cortical thickness, cortical area, and measures of body size as height, weight, and body-mass index, all of them highly heritable. Such false positives can be avoided with permutation tests that respect the family structure.

The figure at the top shows how the subjects of the HCP (terminal dots, shown in white colour) can be shuffled or not, while respecting the family structure. Blue dots indicate branches that can be permuted, whereas red dots indicate branches that cannot (see the main paper for details). This diagram includes 232 subjects of an early public release of HCP data. The tree on the left considers dizygotic twins as a category on their own, i.e., that cannot be shuffled with ordinary siblings, whereas the tree on the right considers dizygotic twins as ordinary siblings.

The first applied study using our strategy has just appeared. The method is implemented in the freely available package PALM — Permutation Analysis of Linear Models, and a set of practical steps to use it with actual HCP data is available here.

References

Van Essen DC, Ugurbil K, Auerbach E, Barch D, Behrens TE, Bucholz R, Chang A, Chen L, Corbetta M, Curtiss SW, Della Penna S, Feinberg D, Glasser MF, Harel N, Heath AC, Larson-Prior L, Marcus D, Michalareas G, Moeller S, Oostenveld R, Petersen SE, Prior F, Schlaggar BL, Smith SM, Snyder AZ, Xu J, Yacoub E; WU-Minn HCP Consortium. The Human Connectome Project: a data acquisition perspective. Neuroimage. 2012;62(4):2222-31.
Van Essen DC, Smith SM, Barch DM, Behrens TEJ, Yacoub E, Ugurbil K. The WU-Minn Human Connectome Project: An overview. Neuroimage. 2013;80:62-79.
Winkler AM, Ridgway GR, Webster MA, Smith SM, Nichols TE. Permutation inference for the general linear model. Neuroimage. 2014;92:381-97. (Open Access)
Winkler AM, Webster MA, Vidaurre D, Nichols TE, Smith SM. Multi-level block permutation. Neuroimage. 2015;123:253-68. (Open Access)

The lady tasting tea experiment

Posted on 23.August.2015 by A. M. Winkler

Can you tell?

The now famous story is that in an otherwise unremarkable summer afternoon in Cambridge in the 1920’s, a group of friends eventually discussed about the claims made by one of the presents about her abilities on discriminating whether milk was poured first or last when preparing a cup of tea with milk. One of the presents was Ronald Fisher, and the story, along with a detailed description of how to conduct a simple experiment to test the claimed ability, and how to obtain an exact solution, was presented at length in the Chapter 2 of his book The Design of Experiments, a few lines of which are quoted below:

A lady declares that by tasting a cup of tea made with milk she can discriminate whether the milk or the tea infusion was first added to the cup. We will consider the problem of designing an experiment by means of which this assertion can be tested. […] [It] consists in mixing eight cups of tea, four in one way and four in the other, and presenting them to the subject for judgment in a random order. The subject has been told in advance of that the test will consist, namely, that she will be asked to taste eight cups, that these shall be four of each kind […]. — Fisher, 1935.

There are $\frac{8!}{4!4!}=70$ distinct possible orderings of these cups, and by telling the subject in advance that there are four cups of each type, this guarantees that the answer will include four of each.

The lady in question eventually answered correctly six out of the eight trials. The results can be assembled in a 2 by 2 contingency table:

		True order:		Total (margin)
		Tea first	Milk first	Total (margin)
Lady’s Guesses:	Tea first	$a=3$	$b=1$	$a+b=4$
Lady’s Guesses:	Milk first	$c=1$	$d=3$	$c+d=4$
Total (margin)		$a+c=4$	$b+d=4$	$n=8$

With these results, what should be concluded about the ability of the lady in discriminating whether milk or tea was poured first? It is not possible to prove that she would never be wrong, because if a sufficiently large number of cups of tea were offered, a single failure would disprove such hypothesis. However, a test that she is never right can be disproven, with a certain margin of uncertainty, given the number of cups offered.

Solution using Fisher’s exact method

Fisher presented an exact solution for this experiment. It is exact in the sense that it allows an exact probability to be assigned to each of the possible outcomes. The probability can be calculated as:

$P_{\text{Fisher}} = \dfrac{(a+b)!(c+d)!(a+c)!(b+d)!}{n!a!b!c!d!}$

For the particular configuration of the contingency table above, the probability is $\frac{16}{70} = 0.22857$ . This is not the final result, though: what matters to disprove the hypothesis that she is not able to discriminate is how likely it would be for her to find a result at least as extreme as the one observed. In this case, there is one case that is more extreme, which would be the one in which she would have made correct guesses for all the 8 cups, in which case the values in the contingency table above would have been $a = 4$ , $b = 0$ , $c = 0$ , and $d = 4$ , with a probability computed with the same formula as $\frac{1}{70} = 0.01429$ . Adding these two probabilities together yield $\frac{16+1}{70}=0.24286$ .

Thus, if the lady is not able to discriminate whether tea or milk was poured first, the chance of observing a result at least as favourable towards her claim would be 0.24286, i.e., about 24%.

If from the outset we were willing to consider a significance level 0.05 (5%) as an informal rule to disprove the null hypothesis, we would have considered the p-value = 0.24286 as non-significant. This p-value is exact, a point that will become more clear below, in the section about permutation tests.

Using the hypergeometric distribution directly

The above process can become laborious for experiments with larger number of trials. An alternative, but equivalent solution, is to appeal directly to the hypergeometric distribution. The probability mass function (pmf) of this distribution can be written as a function the parameters of the contingency table as:

$P(X=a) = \dfrac{\binom{a+b}{a}\binom{c+d}{c}}{\binom{n}{a+c}}$

The pmf is equivalent to Fisher’s exact formula to compute the probability of a particular configuration. The cumulative density function, which is conditional on the margins being fixed, is:

$P(X \geqslant a) = \sum_{j=a}^{J}\dfrac{\binom{a+b}{j}\binom{c+d}{a+c-j}}{\binom{n}{a+c}} = \sum_{j=a}^{J}\dfrac{(a+b)!(c+d)!(a+c)!(b+d)!}{n!j!(a+b-j)!(a+c-j)!(d-a+j)!}$

where $J=\min(a+c,a+b)$ . Computing from the above (details omitted), yield the same value as using Fisher’s presentation, that is, the p-value is (exactly) 0.24286.

Solution using Pearson’s $\chi^2$ method

Much earlier than the tea situation described above, Karl Pearson had already considered the problem of inference in contingency tables, having proposed a test based on a $\chi^2$ statistic.

$\chi^2 = \sum_{i=1}^{R}\sum_{j=1}^{C}\dfrac{(O_{ij}-E_{ij})^2}{E_{ij}}$

where $O_{ij}$ is the observed value for the element in the position $(i,j)$ in the table, $R$ and $C$ are respectively the number of rows and columns, and $E_{ij}$ is the expected value for these elements if the null hypothesis is true. The values $E_{ij}$ can be computed as the product of the marginals for row $i$ and column $j$ , divided by the overall number of observations $n$ . A simpler, equivalent formula is given by:

$\chi^2 = \dfrac{n(ad - bc)^2}{(a+b)(c+d)(a+c)(b+d)}$

A p-value can be computed from the $\chi^2$ distribution with degrees of freedom $\nu=(R-1)(C-1)$ .

Under the null, we can expect a value equal to 2 in each of the 2 cells, that is, the lady would for each cup have a 50:50 chance of answering correctly. For the original tea tasting experiment, Pearson’s method give quite inaccurate results: $\chi^2=2$ , which corresponds to a p-value of 0.07865. However, it is well known that this method is inaccurate if cells in the table have too small quantities, usually below 5 or 6.

Improvement using Yates’ continuity correction

To solve the above well-known issue with small quantities, Yates (1934) proposed a correction, such that the test statistic becomes:

$\chi^2 = \sum_{i,j}\dfrac{\left(|O_{ij}-E_{ij}|-\frac{1}{2}\right)^2}{E_{ij}}$

Applying this correction to the original tea experiment gives $\chi^2=0.5$ , and a p-value of 0.23975, which is very similar to the one given by the Fisher method. Note again that this approach, like the $\chi^2$ test, predates Fisher’s exact test.

Equivalence of Fisher’s exact test and permutation tests

The method proposed by Fisher corresponds to a permutation test. Let $\mathbf{x}$ be a column vector containing binary indicators for whether milk was truly poured first. Let $\mathbf{y}$ be a column vector containing binary indicators for whether the lady answered that milk was poured first. The general linear model (GLM) can be used as usual, such that $\mathbf{y}=\mathbf{x}\beta + \boldsymbol{\epsilon}$ , where $\beta$ is a regression coefficient, and $\boldsymbol{\epsilon}$ are the residuals.

Under the null hypothesis that the lady cannot discriminate, the binary values in $\mathbf{y}$ can be permuted randomly. There are $\binom{8}{4}=70$ possible unique rearrangements. Out of these, in 17, there are 6 or more (out of 8) correct answers matching the values in $\mathbf{x}$ , which gives a p-value 17/70 = 0.24286.

Note that the strategy using the GLM can be used even if both variables $\mathbf{x}$ and $\mathbf{y}$ are binary, as in the example of the tea tasting, even if the residuals are not normally distributed (permutation tests do not depend on distributional assumptions), and even considering that values in $\beta$ can lead to non-sensical predictions in $\mathbf{y}$ , as prediction is not the objective of this analysis.

Why not a binomial test?

The binomial test could be considered if the lady did not know in advance that there were 4 cups of each mixture order. Since she knew (so the two margins of the table are fixed), each cup was not independent from each other, and her possible answers had to be constrained by answers previously given. The binomial test assumes independence, thus, is not an option for this analysis.

Relevance

Using this simple experiment, Fisher established most of the fundamental principles for hypothesis testing, which contributed to major advances across biological and physical sciences. A careful read of the original text shows a precise use of terms, in a concise and unambiguous presentation, in contrast with many later and more verbose textbooks that eventually hid from readers most of the fundamental principles.

References

Fisher, R. A. The Design of Experiments. Oliver and Boyd, Edinburgh, 1935.
Pearson K. X. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Philos Mag Ser 5. 1900 Jul;50(302):157–75.
Yates F. Contingency Tables Involving Small Numbers and the Chi^2 test. Suppl to J R Stat Soc. 1934;1(2):217–35.

The photograph at the top (tea with milk) is in public domain.

The G-statistic

Posted on 17.February.2014 by A. M. Winkler

Preliminaries

Consider the common analysis of a neuroimaging experiment. At each voxel, vertex, face or edge (or any other imaging unit), we have a linear model expressed as:

$\mathbf{Y} = \mathbf{M} \boldsymbol{\psi} + \boldsymbol{\epsilon}$

where $\mathbf{Y}$ contains the experimental data, $\mathbf{M}$ contains the regressors, $\boldsymbol{\psi}$ the regression coefficients, which are to be estimated, and $\boldsymbol{\epsilon}$ the residuals. For a linear null hypothesis $\mathcal{H}_0 : \mathbf{C}'\boldsymbol{\psi}=\mathbf{0}$ , where $\mathbf{C}$ is a contrast. If $\mathsf{rank}\left(\mathbf{C}\right) = 1$ , the Student’s t statistic can be calculated as:

$t = \boldsymbol{\hat{\psi}}'\mathbf{C} \left(\mathbf{C}'(\mathbf{M}'\mathbf{M})^{-1}\mathbf{C} \right)^{-\frac{1}{2}} \left/ \sqrt{\dfrac{\boldsymbol{\hat{\epsilon}}'\boldsymbol{\hat{\epsilon}}}{N-\mathsf{rank}\left(\mathbf{M}\right)}} \right.$

where the hat on $\boldsymbol{\hat{\psi}}$ and $\boldsymbol{\hat{\epsilon}}$ indicate that these are quantities estimated from the sample. If $\mathsf{rank}\left(\mathbf{C}\right) \geqslant 1$ , the F statistic can be obtained as:

$F = \left.\dfrac{\boldsymbol{\hat{\psi}}'\mathbf{C} \left(\mathbf{C}'(\mathbf{M}'\mathbf{M})^{-1}\mathbf{C} \right)^{-1} \mathbf{C}'\boldsymbol{\hat{\psi}}}{\mathsf{rank}\left(\mathbf{C}\right)} \right/ \dfrac{\boldsymbol{\hat{\epsilon}}'\boldsymbol{\hat{\epsilon}}}{N-\mathsf{rank}\left(\mathbf{M}\right)}$

When $\mathsf{rank}\left(\mathbf{C}\right) = 1$ , $F = t^2$ . For either of these statistics, we can assess their significance by repeating the same fit after permuting $\mathbf{Y}$ or $\mathbf{M}$ (i.e., a permutation test), or by referring to the formula for the distribution of the corresponding statistic, which is available in most statistical software packages (i.e., a parametric test).

Permutation tests don’t depend on the same assumptions on which parametric tests are based. As some of these assumptions can be quite stringent in practice, permutation methods arguably should be preferred as a general framework for the statistical analysis of imaging data. At each permutation, a new statistic is computed and used to build its empirical distribution from which the p-values are obtained. In practice it’s not necessary to build the full distribution, and it suffices to increment a counter at each permutation. At the end, the counter is divided by the number of permutations to produce a p-value.

An example of a permutation distribution

Using permutation tests, correction for multiple testing using the family-wise error rate (fwer) is trivial: rather than build the permutation distribution at each voxel, a single distribution of the global maximum of the statistic across the image is constructed. Each permutation yields one maximum, that is used to build the distribution. Any dependence between the tests is implicitly captured, with not need to model it explicitly, nor to introduce even more assumptions, a problem that hinders methods such as the random field theory.

Exchangeability blocks

Permutation is allowed if it doesn’t affect the joint distribution of the error terms, i.e., if the errors are exchangeable. Some types of experiments may involve repeated measurements or other kinds of dependency, such that exchangeability cannot be guaranteed between all observations. However, various cases of structured dependency can still be accommodated if sets (blocks) of observations are shuffled as a whole, or if shuffling happens only within set (block). It is not necessary to know or to model the exact dependence structure between observations, which is captured implicitly as long as the blocks are defined correctly.

Permutation within block.

Permutation of blocks as a whole.

The two figures above are of designs constructed using the fsl software package. In fsl, within-block permutation is available in randomise with the option -e, used to supply a file with the definition of blocks. For whole-block permutation, in addition to the option -e, the option --permuteBlocks needs to be supplied.

The G-statistic

The presence of exchangeability blocks solves a problem, but creates another. Having blocks implies that observations may not be pooled together to produce a non-linear parameter estimate such as the variance. In other words: the mere presence of exchangeability blocks, either for shuffling within or as a whole, implies that the variances may not be the same across all observations, and a single estimate of this variance is likely to be inaccurate whenever the variances truly differ, or if the groups don’t have the same size. This also means that the F or t statistics may not behave as expected.

The solution is to use the block definitions and the permutation strategy is to define groups of observations that are known or assumed to have identical variances, and pool only the observations within group for variance estimation, i.e., to define variance groups (vgs).

The F-statistic, however, doesn’t allow such multiple groups of variances, and we need to resort to another statistic. In Winkler et al. (2014) we propose:

$G = \dfrac{\boldsymbol{\hat{\psi}}'\mathbf{C} \left(\mathbf{C}'(\mathbf{M}'\mathbf{W}\mathbf{M})^{-1}\mathbf{C} \right)^{-1} \mathbf{C}'\boldsymbol{\hat{\psi}}}{\Lambda \cdot s}$

where $\mathbf{W}$ is a diagonal matrix that has elements:

$W_{nn}=\dfrac{\sum_{n' \in g_{n}}R_{n'n'}}{\boldsymbol{\hat{\epsilon}}_{g_{n}}'\boldsymbol{\hat{\epsilon}}_{g_{n}}}$

and where $R_{n'n'}$ are the $n'$ diagonal elements of the residual forming matrix, and $g_{n}$ is the variance group to which the $n$ -th observation belongs. The remaining denominator term, $\Lambda$ , is given by (Welch, 1951):

$\Lambda = 1+\frac{2(s-1)}{s(s+2)}\sum_{g} \frac{1}{\sum_{n \in g}R_{nn}} \left(1-\frac{\sum_{n \in g}W_{nn}}{\mathsf{trace}\left(\mathbf{W}\right)}\right)^2$

where $s=\mathsf{rank}\left(\mathbf{C}\right)$ . The matrix $\mathbf{W}$ can be seen as a weighting matrix, the square root of which normalises the model such that the errors have then unit variance and can be ignored. It can also be seen as being itself a variance estimator. In fact, it is the very same variance estimator proposed by Horn et al (1975).

The W matrix used with the G statistic. It is constructed from the estimated variances of the error terms.

The matrix $\mathbf{W}$ has a crucial role in making the statistic pivotal in the presence of heteroscedasticity. Pivotality means that the statistic has a sampling distribution that is not dependent on any unknown parameter. For imaging experiments, it’s important that the statistic has this property, otherwise correction for multiple testing that controls fwer will be inaccurate, or possibly invalid altogether.

When $\mathsf{rank}\left(\mathbf{C}\right)=1$ , the t-equivalent to the G-statistic is $v = \boldsymbol{\hat{\psi}}'\mathbf{C} \left(\mathbf{C}'(\mathbf{M}'\mathbf{W}\mathbf{M})^{-1}\mathbf{C} \right)^{-\frac{1}{2}}$ , which is the well known Aspin-Welch $v$ -statistic for the Behrens-Fisher problem. The relationship between $v$ and G is the same as between t and F, i.e., when the rank of the contrast equals to one, the latter is simply the square of the former. The G statistic is a generalization of all these, and more, as we show in the paper, and summarise in the table below:

	$\mathsf{rank}\left(\mathbf{C}\right) = 1$	$\mathsf{rank}\left(\mathbf{C}\right) > 1$
Homoscedastic errors, unrestricted exchangeability	Square of Student’s t	F-ratio
Homoscedastic within vg, restricted exchangeability	Square of Aspin-Welch $v$	Welch’s $v^2$

In the absence of variance groups (i.e., all observations belong to the same vg), G and $v$ are equivalent to F and t respectively.

Although not typically necessary if permutation methods are to be preferred, approximate parametric p-values for the G-statistic can be computed from an F-distribution with $\nu_1=s$ and $\nu_2=2(s-1)/3/(\Lambda-1)$ .

While the error rates are controlled adequately (a feature of permutation tests in general), the G-statistic offers excellent power when compared to the F-statistic, even when the assumptions of the latter are perfectly met. Moreover, by preserving pivotality, it is an adequate statistic to control of the error rate in the in the presence of multiple tests.

In this post, the focus is in using G for imaging data, but of course, it can be used for any dataset in which a linear model where variances cannot be assumed to be the same is used, i.e., when heteroscedasticity is or could be present.

Note that the G-statistic has nothing to do with the G-test. It is named as this for being a generalisation over various tests, including the commonly used t and F tests, as shown above.

Main reference

The core reference and results for the G-statistic have just been published in Neuroimage:

Winkler AM, Ridgway GR, Webster MA, Smith SM, Nichols TE. Permutation inference for the general linear model. Neuroimage. 2014;92:381-397

Other references

The two other references cited, which are useful to understand the variance estimator and the parametric approximation are:

Horn S, Horn R, Duncan D. Estimating heteroscedastic variances in linear models. J Am Stat Assoc. 1975;70(350):380–385.
Welch B. On the comparison of several mean values: an alternative approach. Biometrika. 1951;38(3):330–336.

Biased, as it should be

Posted on 12.April.2013 by A. M. Winkler

When we run a permutation test, what we do is to first compute the statistic for the unpermuted model, then shuffle the data randomly, compute a new statistic and, if it is larger than the statistic for the unpermuted model, increment a counter. We then repeat the random shuffling, and keep incrementing the counter until we think we are done with them. We then divide the counter by the number of permutations and the result is the p-value what we wanted to find.

This procedure can be stated as:

$\hat{p} = \frac{1}{N}\sum^{N}_{n=1}\mathcal{I}(T^{*}_{n} \geqslant T_0)$

where $\hat{p}$ is the estimated p-value, $N$ is the number of permutations, $T_0$ is the statistic for the unpermuted model, $T^{*}_n$ is the statistic for the $n$ -th random shuffling, and $\mathcal{I}$ is an indicator function that evaluates as 1 if the condition between parenthesis is true, or 0 otherwise. This formulation produces unbiased results: since $E(\mathcal{I}(T^{*}_{n} \geqslant T_0)) = p$ , the true p-value, then $E(\frac{1}{N}\sum^{N}_{n=1}\mathcal{I}(T^{*}_{n} \geqslant T_0)) = p$ .

The problem

This strategy, however, has a problem. If the true p-value, $p$ , is small, or if the number of permutations is not sufficiently large, even after all the $N$ permutations are done, no $T^{*}_{n}$ may reach or surpass the value of $T_0$ , resulting in a p-value equal to 0. While this is still a valid, unbiased result, p-values equal to zero are problematic, as they can be interpreted as indicating the rejection of the null-hypothesis with absolute confidence. And this even after very few permutations (perhaps just 1!) have been performed, which is indeed rather counter-intuitive. We cannot be completely sure of the rejection of the null simply for having done just a few permutations.

Biasing to solve the problem

The solution is to make two modifications to the formulation above: start counting the $n$ -th permutation at 0, for the unpermuted model, and divide the counter at the end not by $N$ , but by $N+1$ :

$\hat{p} = \frac{1}{N+1}\sum^{N}_{n=0}\mathcal{I}(T^{*}_{n} \geqslant T_0)$

This formulation, which pools the unpermuted model together with the permuted realisations, is biased: for $n=0$ , $\mathcal{I}(T^{*}_{n} \geqslant T_0) = 1$ , and so, $E(\frac{1}{N+1}\sum^{N}_{n=0}\mathcal{I}(T^{*}_{n} \geqslant T_0)) = \frac{1+Np}{N+1} \neq p$ .

Quantifying the bias

The bias is smaller for a large number of permutations, and converges to zero as $N$ increases towards infinity. What is important, however, is that the bias punishes the results towards conservativeness whenever the true and unknown $p$ is smaller than $\frac{1}{N+1}$ , in a way that no p-value smaller than $\frac{1}{N+1}$ can ever be attained. It forces the researcher to run more permutations to find such small p-values to reject the null hypothesis, which otherwise could be rejected with a p-value equal to zero that would appear easily even after just a handful of permutations.

The bias is larger for smaller number of permutations and for smaller true p-values.

Controversy

The solution has been proposed by some authors, such as Edgington (1995), and strongly advocated by, e.g., Phipson and Smyth (2010). While the biased solution is definitely the most adequate for practical scientific problems, it can be considered as of little actual statistical meaning. Pesarin and Salmaso (2010) explain that the distribution of $T_0$ is not the same as the distribution of $T^{*}_{n}$ , unless the null is true. Under the alternative hypothesis, therefore, $T_0$ should not be pooled into the empirical distribution from which the p-value is obtained. Moreover, under the null, all possible permutations have the same probability, with no intrinsic reason to treat some (as the unpermuted) differently than others. If one wants unbiased results, the alternative formulation should obviously not be used.