Extreme values are useful to quantify the risk of catastrophic floods, and much more.
This is a brief set of notes with an introduction to extreme value theory. For reviews, see Leadbetter et al (1983) and David and Huser (2015) [references at the end]. Also of some (historical) interest might be the classical book by Gumbel (1958). Let 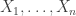 be a sequence of independent and identically distributed variables with cumulative distribution function (cdf)
be a sequence of independent and identically distributed variables with cumulative distribution function (cdf) 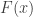 and let
and let 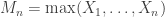 denote the maximum.
denote the maximum.
If 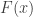 is known, the distribution of the maximum is:
is known, the distribution of the maximum is:

The distribution function 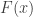 might, however, not be known. If data are available, it can be estimated, although small errors on the estimation of
might, however, not be known. If data are available, it can be estimated, although small errors on the estimation of 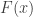 can lead to large errors concerning the extreme values. Instead, an asymptotic result is given by the extremal types theorem, also known as Fisher-Tippett-Gnedenko Theorem, First Theorem of Extreme Values, or extreme value trinity theorem (called under the last name by Picklands III, 1975).
can lead to large errors concerning the extreme values. Instead, an asymptotic result is given by the extremal types theorem, also known as Fisher-Tippett-Gnedenko Theorem, First Theorem of Extreme Values, or extreme value trinity theorem (called under the last name by Picklands III, 1975).
But before that, let’s make a small variable change. Working with 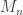 directly is problematic because as
directly is problematic because as  ,
, 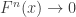 . Redefining the problem as a function of
. Redefining the problem as a function of 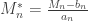 renders treatment simpler. The theorem can be stated then as: If there exist sequences of constants
renders treatment simpler. The theorem can be stated then as: If there exist sequences of constants  and
and  such that, as
such that, as  :
:
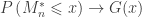
then 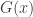 belongs to one of three “domains of attraction”:
belongs to one of three “domains of attraction”:
- Type I (Gumbel law):
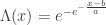 , for
, for 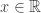 indicating that the distribution of
indicating that the distribution of 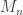 has an exponential tail.
has an exponential tail.
- Type II (Fréchet law):
 indicating that the distribution of
indicating that the distribution of  has a heavy tail (including polynomial decay).
has a heavy tail (including polynomial decay).
- Type III (Weibull law):
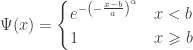 indicating that the distribution of
indicating that the distribution of 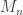 has a light tail with finite upper bound.
has a light tail with finite upper bound.
Note that in the above formulation, the Weibull is reversed so that the distribution has an upper bound, as opposed to a lower one as in the Weibull distribution. Also, the parameterisation is slightly different than the one usually adopted for the Weibull distribution.
These three families have parameters 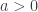 ,
,  and, for families II and III,
and, for families II and III,  . To which of the three a particular
. To which of the three a particular 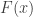 is attracted is determined by the behaviour of the tail of of the distribution for large
is attracted is determined by the behaviour of the tail of of the distribution for large  . Thus, we can infer about the asymptotic properties of the maximum while having only a limited knowledge of the properties of
. Thus, we can infer about the asymptotic properties of the maximum while having only a limited knowledge of the properties of 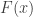 .
.
These three limiting cases are collectively termed extreme value distributions. Types II and III were identified by Fréchet (1927), whereas type I was found by Fisher and Tippett (1928). In his work, Fréchet used  , whereas Fisher and Tippett used
, whereas Fisher and Tippett used 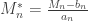 . Von Mises (1936) identified various sufficient conditions for convergence to each of these forms, and Gnedenko (1943) established a complete generalisation.
. Von Mises (1936) identified various sufficient conditions for convergence to each of these forms, and Gnedenko (1943) established a complete generalisation.
Generalised extreme value distribution
As shown above, the rescaled maxima converge in distribution to one of three families. However, all are cases of a single family that can be represented as:
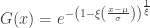
defined on the set  , with parameters
, with parameters  (location),
(location),  (scale), and
(scale), and 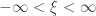 (shape). This is the generalised extreme value (GEV) family of distributions. If
(shape). This is the generalised extreme value (GEV) family of distributions. If 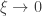 , it converges to Gumbel (type I), whereas if
, it converges to Gumbel (type I), whereas if 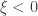 it corresponds to Fréchet (type II), and if
it corresponds to Fréchet (type II), and if  it corresponds to Weibull (type III). Inference on
it corresponds to Weibull (type III). Inference on 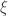 allows choice of a particular family for a given problem.
allows choice of a particular family for a given problem.
Generalised Pareto distribution
For 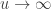 , the limiting distribution of a random variable
, the limiting distribution of a random variable  , conditional on
, conditional on 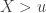 , is:
, is:
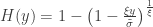
defined for  and
and 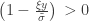 . The two parameters are the
. The two parameters are the 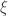 (shape) and
(shape) and 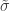 (scale). The shape corresponds to the same parameter
(scale). The shape corresponds to the same parameter 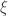 of the GEV, whereas the scale relates to the scale of the former as
of the GEV, whereas the scale relates to the scale of the former as 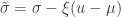 .
.
The above is sometimes called the Picklands-Baikema-de Haan theorem or the Second Theorem of Extreme Values, and it defines another family of distributions, known as generalised Pareto distribution (GPD). It generalises an exponential distribution with parameter 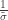 as
as 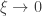 , an uniform distribution in the interval
, an uniform distribution in the interval ![\left[0, \tilde{\sigma}\right]](https://s0.wp.com/latex.php?latex=%5Cleft%5B0%2C+%5Ctilde%7B%5Csigma%7D%5Cright%5D&bg=ffffff&fg=333333&s=0&c=20201002) when
when 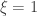 , and a Pareto distribution when
, and a Pareto distribution when  .
.
Parameter estimation
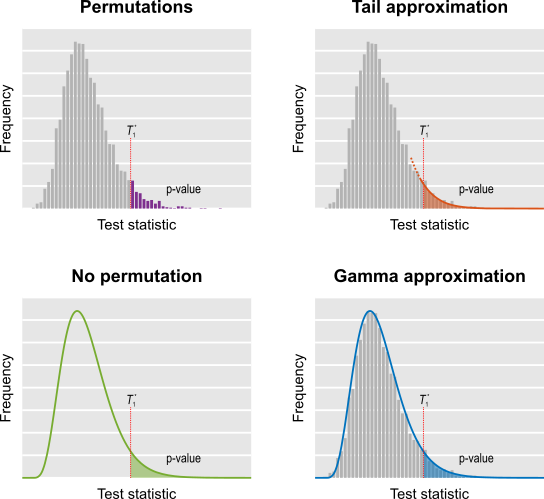
By restricting the attention to the most common case of  , which represent distributions approximately exponential, parametters for the GPD can be estimated using at least three methods: maximum likelihood, moments, and probability-weighted moments. These are described in Hosking and Wallis (1987). For
, which represent distributions approximately exponential, parametters for the GPD can be estimated using at least three methods: maximum likelihood, moments, and probability-weighted moments. These are described in Hosking and Wallis (1987). For 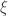 outside this interval, methods have been discussed elsewhere (Oliveira, 1984). The method of moments is probably the simplest, fastest and, according to Hosking and Wallis (1987) and Knijnenburg et al (2009), has good performance for the typical cases of
outside this interval, methods have been discussed elsewhere (Oliveira, 1984). The method of moments is probably the simplest, fastest and, according to Hosking and Wallis (1987) and Knijnenburg et al (2009), has good performance for the typical cases of  .
.
For a set of extreme observations, let 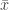 and
and 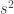 be respectively the sample mean and variance. The moment estimators of
be respectively the sample mean and variance. The moment estimators of 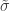 and
and 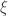 are
are  and
and  .
.
The accuracy of these estimates can be tested with, e.g., the Anderson-Darling goodness-of-fit test (Anderson and Darling, 1952; Choulakian and Stephens, 2001), based on the fact that, if the modelling is accurate, the p-values for the distribution should be uniformly distributed.
Availability
Statistics of extremes are used in PALM as a way to accelerate permutation tests. More details to follow soon.
References
- Anderson TW, Darling DA. Asymptotic theory of certain goodness of fit criteria based on stochastic processes. Ann Math Stat. 1952;23(2):193-212.
- Choulakian V, Stephens MA. Goodness-of-Fit Tests for the Generalized Pareto Distribution. Technometrics. 2001;43(4):478-84.
- Davison AC, Huser R. Statistics of Extremes. Annu Rev Stat Its Appl. 2015;2(1):203-35.
- Fisher RA, Tippett LHC. Limiting forms of the frequency distribution of the largest and smallest member of a sample. Proc Camb Philol Soc. 1928;24:180-90.
- Fréchet, M. Sur la loi de probabilité de l’écart maximum. Ann Soc Polon Math. 1927;6:93. [link currently not accessible due to copyright issues]
- Gnedenko B. Sur La Distribution Limite Du Terme Maximum D’Une Serie Aleatoire. Ann Math. 1943;44(3):423-53.
- Gumbel E. Statistics of Extremes. Echo Point Books & Media, 1958.
- Hosking JRM, Wallis JR. Parameter and quantile estimation for the generalized Pareto distribution. Technometrics. 1987;29:339-49.
- Knijnenburg TA, Wessels LFA, Reinders MJT, Shmulevich I. Fewer permutations, more accurate P-values. Bioinformatics. 2009 Jun 15;25(12):i161-8.
- Leadbetter MR, Lindgren G, Rootzén H. Extremes and related properties of
random sequences and processes. Springer-Verlag, New York, 1983.
- Oliveira JT (ed). Proceedings of the NATO Advanced Study Institute on Statistical Extremes and Applications. D. Heidel, Dordrecht, Holland, 1984.
- Picklands III J. Statistical inference using extreme order statistics. Ann Stat. 1975;3(1):119-31.
- Tippett LHC. On the extreme individuals and the range of samples taken from a normal population. Biometrika. 1925;17(3):364-87.
- von Mises R. La distribution de la plus grande de n valeurs. Rev Mathématique l’Union Interbalkanique. 1936;1:141-60.
The figure at the top (flood) is in public domain.