Permutation tests are more robust and help to make scientific results more reproducible by depending on fewer assumptions. However, they are computationally intensive as recomputing a model thousands of times can be slow. The purpose of this post is to briefly list some options available for speeding up permutation.

Firstly, no speed-ups may be needed: for small sample sizes, or low resolutions, or small regions of interest, a permutation test can run in a matter of minutes. For larger data, however, accelerations may be of use. One option is acceleration through parallel processing or GPUs (for example applications of the latter, see Eklund et al., 2012, Eklund et al., 2013 and Hernández et al., 2013; references below), though this does require specialised implementation. Another option is to reduce the computational burden by exploiting the properties of the statistics and their distributions. A menu of options includes:

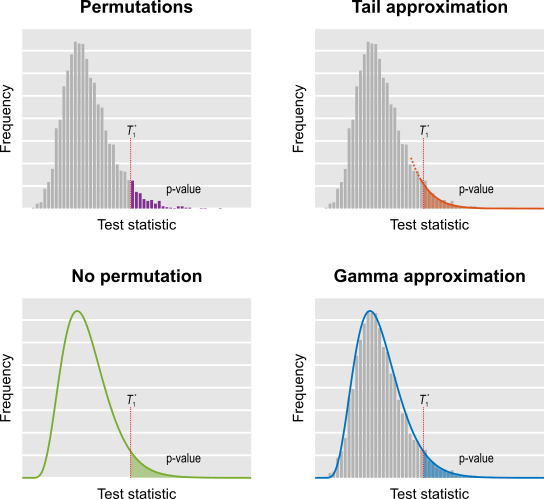
• Do few permutations (shorthand name: fewperms). The results remain valid on average, although the p-values will have higher variability.
• Keep permuting until a fixed number of permutations with statistic larger than the unpermuted is found (a.k.a., negative binomial; shorthand name: negbin).
• Do a few permutations, then approximate the tail of the permutation distribution by fitting a generalised Pareto distribution to its tail (shorthand name: tail).
• Approximate the permutation distribution with a gamma distribution, using simple properties of the test statistic itself, amazingly not requiring any permutations at all (shorthand name: noperm).
• Do a few permutations, then approximate the full permutation distribution by fitting a gamma distribution (shorthand name: gamma).
• Run permutations on only a few voxels, then fill the missing ones using low-rank matrix completion theory (shorthand name: lowrank).

These strategies allow accelerations >100x, yielding nearly identical results as in the non-accelerated case. Some, such as tail approximation, are generic enough to be used nearly all the most common scenarios, including univariate and multivariate tests, spatial statistics, and for correction for multiple testing.

In addition to accelerating permutation tests, some of these strategies, such as tail and noperm, allow continuous p-values to be found, and refine the p-values far into the tail of the distribution, thus avoiding the usual discreteness of p-values, which can be a problem in some applications if too few permutations are done.

These methods are available in the tool PALM — Permutation Analysis of Linear Models — and the complete description, evaluation, and application to the re-analysis of a voxel-based morphometry study (Douaud et al., 2007) have been just published in Winkler et al., 2016 (for the Supplementary Material, click here). The paper includes a flow chart prescribing these various approaches for each case, reproduced below.

The hope is that these accelerations will facilitate the use of permutation tests and, if used in combination with hardware and/or software improvements, can further expedite computation leaving little reason not to use these tests.

References

• Douaud G, Smith S, Jenkinson M, Behrens T, Johansen-Berg H, Vickers J, James S, Voets N, Watkins K, Matthews PM, James A. Anatomically related grey and white matter abnormalities in adolescent-onset schizophrenia. Brain. 2007 Sep;130(Pt 9):2375-86. Epub 2007 Aug 13.
• Eklund A, Andersson M, Knutsson H. fMRI analysis on the GPU-possibilities and challenges. Comput Methods Programs Biomed. 2012 Feb;105(2):145-61.
• Eklund A, Dufort P, Forsberg D, LaConte SM. Medical image processing on the GPU – Past, present and future. Med Image Anal. 2013;17(8):1073-94.
• Hernández M, Guerrero GD, Cecilia JM, García JM, Inuggi A, Jbabdi S, et al. Accelerating fibre orientation estimation from diffusion weighted magnetic resonance imaging using GPUs. PLoS One. 2013 Jan;8(4):e61892.1.
• Winkler AM, Ridgway GR, Webster MA, Smith SM, Nichols TE. Permutation inference for the general linear model. Neuroimage. 2014 May 15;92:381-97.
• Winkler AM, Ridgway GR, Douaud G, Nichols TE, Smith SM. Faster permutation inference in brain imaging. Neuroimage. 2016 Jun 7;141:502-516.

Contributed to this post: Tom Nichols, Ged Ridgway.