Log-normality and the Box-Cox transformation

Posted on 17.July.2011 by A. M. Winkler

The Box-Cox transformation (Box and Cox, 1964) is a way to transform data that ordinarily do not follow to a normal distribution so that it then conforms to it. The transformation is a piecewise function of the power parameter $\lambda$ :

The function is, given the definition, continuous at the singular point $\lambda = 0$ . Plotting the transformation as a function of the original data $y$ and the parameter $\lambda$ produces the following:

An interesting aspect of the Box-Cox transformation is that it can be used as a metric to quantify how normal or log-normal certain data are. This has clear applications in biology. Tissue growth that depends on cellular multiplication is exponential, with a constant factor that is often normally distributed, resulting in tissue size that is log-normally distributed (for discussion, see McAlister, 1879; Koch, 1966; Koch, 1969). Measurements of the final tissue size in different individuals, however, may not perfectly conform to the log-normal due to external influences that may hinder tissue growth. Moreover, it is not always possible to measure the final amount of tissue that is the product of a single lineage of self-multiplicative cells. The combination of different cell lineages, each with their own growth rate, as well as external influences, tend to produce a distribution that is more normally (Gaussianly) distributed. A distribution gradient, therefore, may exist between these two extremes of normality and log-normality. Estimating the parameter $\lambda$ allows one to estimate also how closer to normal or log-normal certain measurements are. If $\lambda \approx 0$ , the original data tend to be log-normally distributed, whereas if $\lambda \approx +1$ , the data can be considered approximately more normally distributed.

References

Box GEP, Cox DR. An analysis of transformations. J R Stat Soc B. 1964; 26(2):211-52.
Koch AL. The logarithm in biology. 1. Mechanisms generating the log-normal distribution exactly. J Theor Biol. 1966; 12(2):276-90.
Koch AL. The logarithm in biology. II. Distributions simulating the log-normal. J Theor Biol. 1969; 23(2):251-68.
McAlister D. The law of the geometric mean. Proc R Soc London. 1879; 29:367-76.

Inverse normal transformation in SOLAR

Posted on 13.July.2011 by A. M. Winkler

SOLAR software can, at the discretion of the user, apply a rank-based inverse-normal transformation to the data using the command inormal. This transformation is the one suggested by Van der Waerden (1952) and is given by:

$\tilde y_i = \Phi^{-1}\left\{\dfrac{r_i}{n+1}\right\}$

where $\tilde y_i$ is the transformed value for observation $i$ , $\Phi^{-1}\left\{\cdot\right\}$ is the probit function, $r_i$ is the ordinary rank of the $i$ -th case among $n$ observations.

This transformation is a particular case of the family of transformations discussed in the paper by Beasley et al. (2009). The family can be represented as:

$\tilde y_i = \Phi^{-1}\left\{\dfrac{r_i+c}{n-2c+1}\right\}$

where $c$ is a constant and the remaining variables are as above. The value of $c$ varies for different proposed methods. Blom (1958) suggests $c=3/8$ , Tukey (1962) suggests $c=1/3$ , Bliss (1967) suggests $c=1/2$ and, as just decribed, Van der Waerden suggests $c=0$ .

Interesting enough, the Q-Q plots produced by Octave use the Bliss (1967) transformation.

An Octave/matlab function to perform these transformations in arbitrary data is here: inormal.m (note that this function does not require or use SOLAR).

References

Van der Waerden BL. Order tests for the two-sample problem and their power. Proc Koninklijke Nederlandse Akademie van Wetenschappen. Ser A. 1952; 55:453–458.
Blom G. Statistical estimates and transformed beta-variables. Wiley, New York, 1958 (page 71).
Tukey JW. The future of data analysis. Ann Math Stat. 1962; 33:1–67.
Bliss CI. Statistics in biology. McGraw-Hill, New York, 1967 (pages 117–120).
Beasley TM, Erickson S, Allison DB. Rank-based inverse normal transformations are increasingly used, but are they merited? Behav Genet. 2009; 39(5):580-95.

Version history

23.Jul.2011: First public release.
19.Jun.2014: Added ability to deal with ties, as well as NaNs in the data.

Normality tests II: Asymptotic approximations

Posted on 07.July.2011 by A. M. Winkler

In the previous post, the procedures to compute a statistic for six common normality tests and how to obtain the respective p-values using asymptotic approximations were briefly reviewed. In this post, it is shown that these approximations, that appear in classic statistical textbooks and papers, are not entirely accurate for arbitrary sample sizes or nominal levels of significance.

For each test, 1,000,000 realisations of normal distributions were simulated using matlab, computed analytically the p-values, and plotted their frequencies at significance intervals of 0.01, with 34 different sample sizes, ranging from 10 to 10,000 (more specifically: 10, 15, 20, 25, 30, 40, 50, 60, 70, 80, 90, 100, 150, 200, 250, 300, 400, 500, 600, 700, 800, 900, 1000, 1500, 2000, 2500, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10000). The best approximations should produce flat series of bars between p-values 0-1, and be stable across sample sizes, particularly at the most common significance levels: near or below p=0.05.

In general, any test can be analysed according to power, robustness to sample size, ability to correctly reject some specific types of distributions and other parameters. The analyses presented here refer exclusively to the ability to reject the null when the null is true at the nominal significance level using analytical approximations. Poor performance in this analysis does not imply that the test, per se, is poor. It only implies that the approximation used to derive the p-values is not accurate. The tests may still be very powerful to detect non-normality, but accurate p-values must then rely on tables produced via Monte Carlo simulations, which are, by definition, always exact.

Skewness test

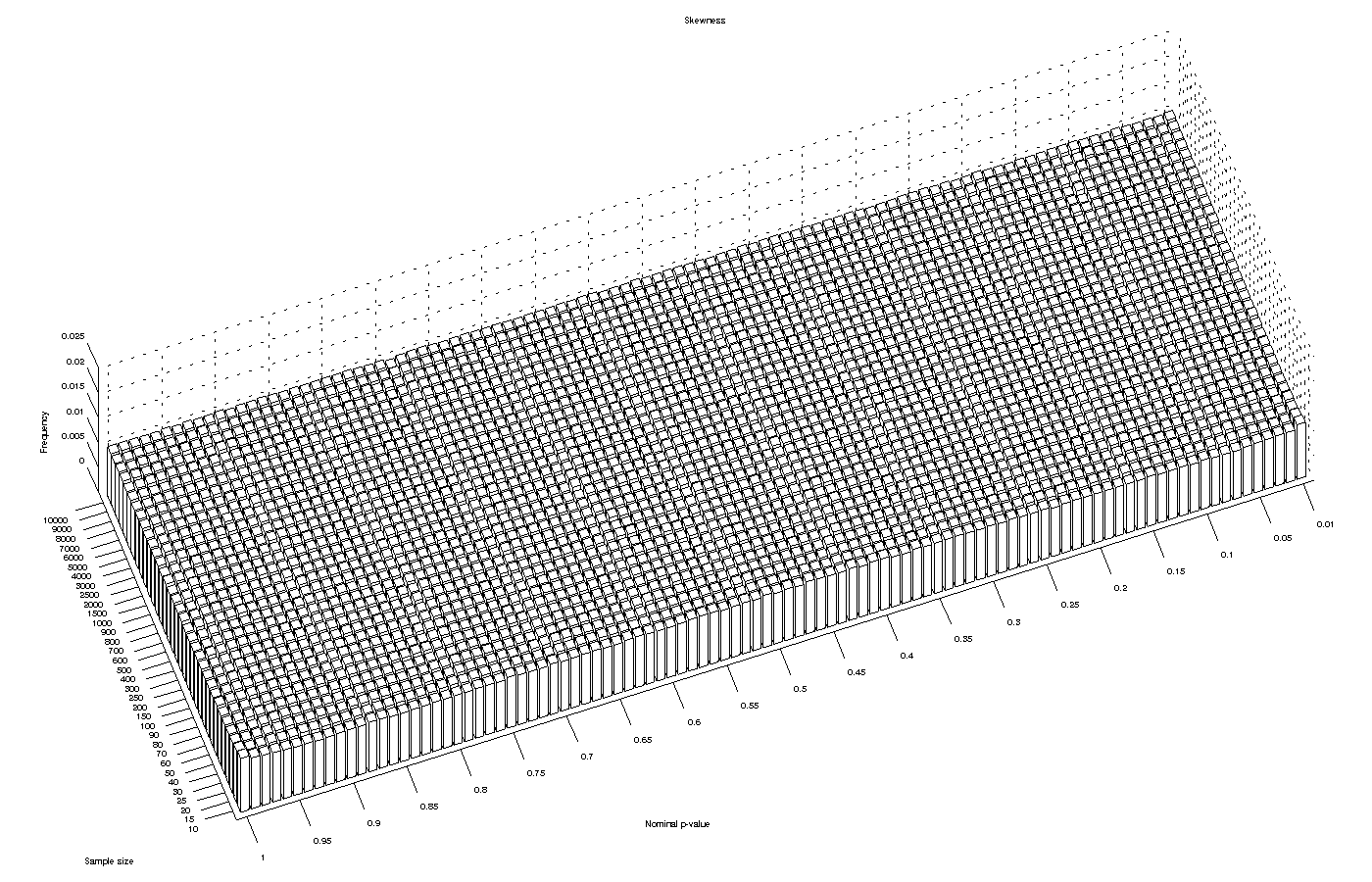
The skewness test is perhaps the one that performed better in terms of asymptotic approximation to a p-value (which does not imply that this test is at all more powerful or has any other feature that would qualify it as better than the others). The approximation produces p-values that are virtually identical to the nominal p-values for any of the sample sizes.

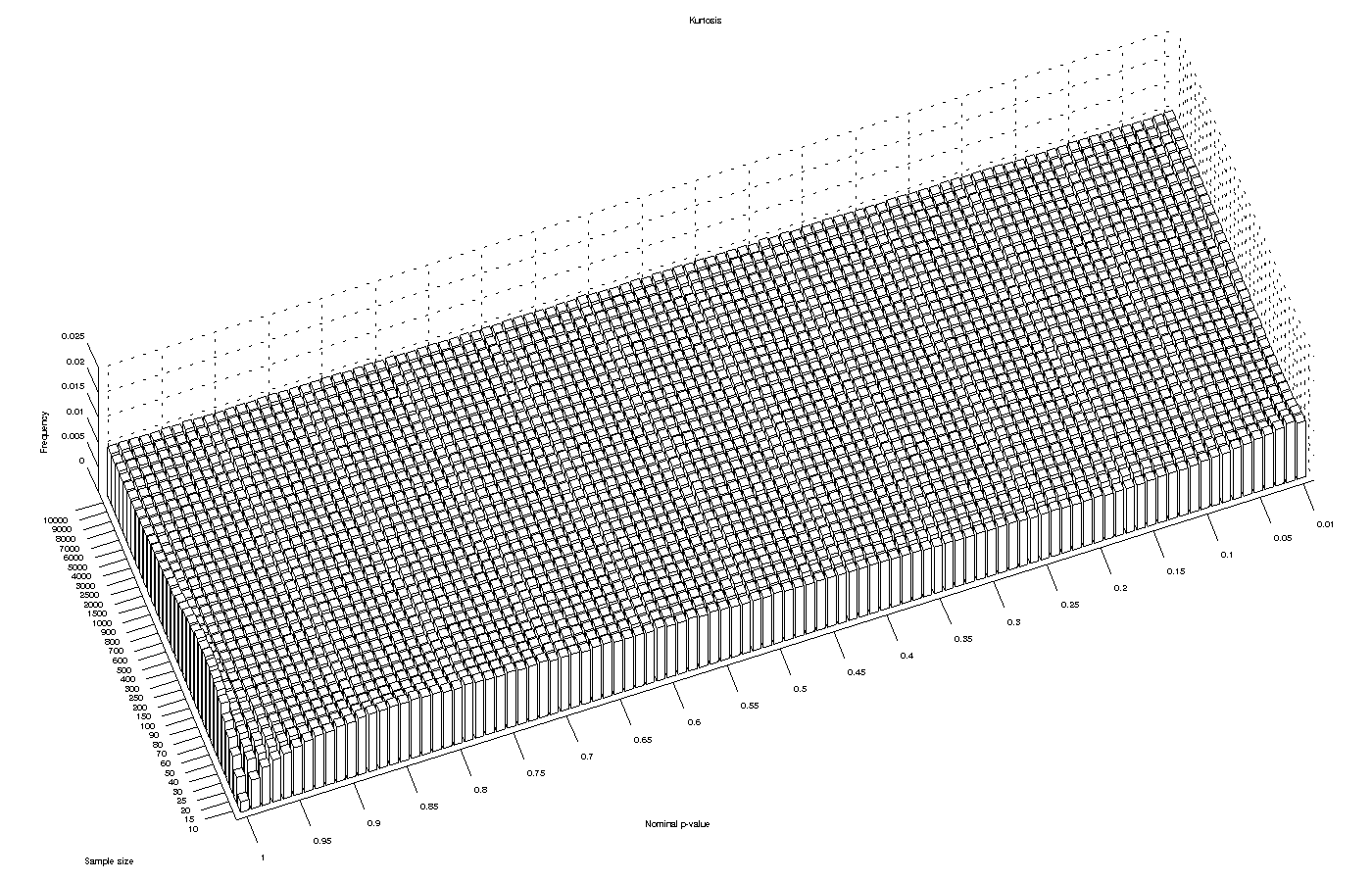
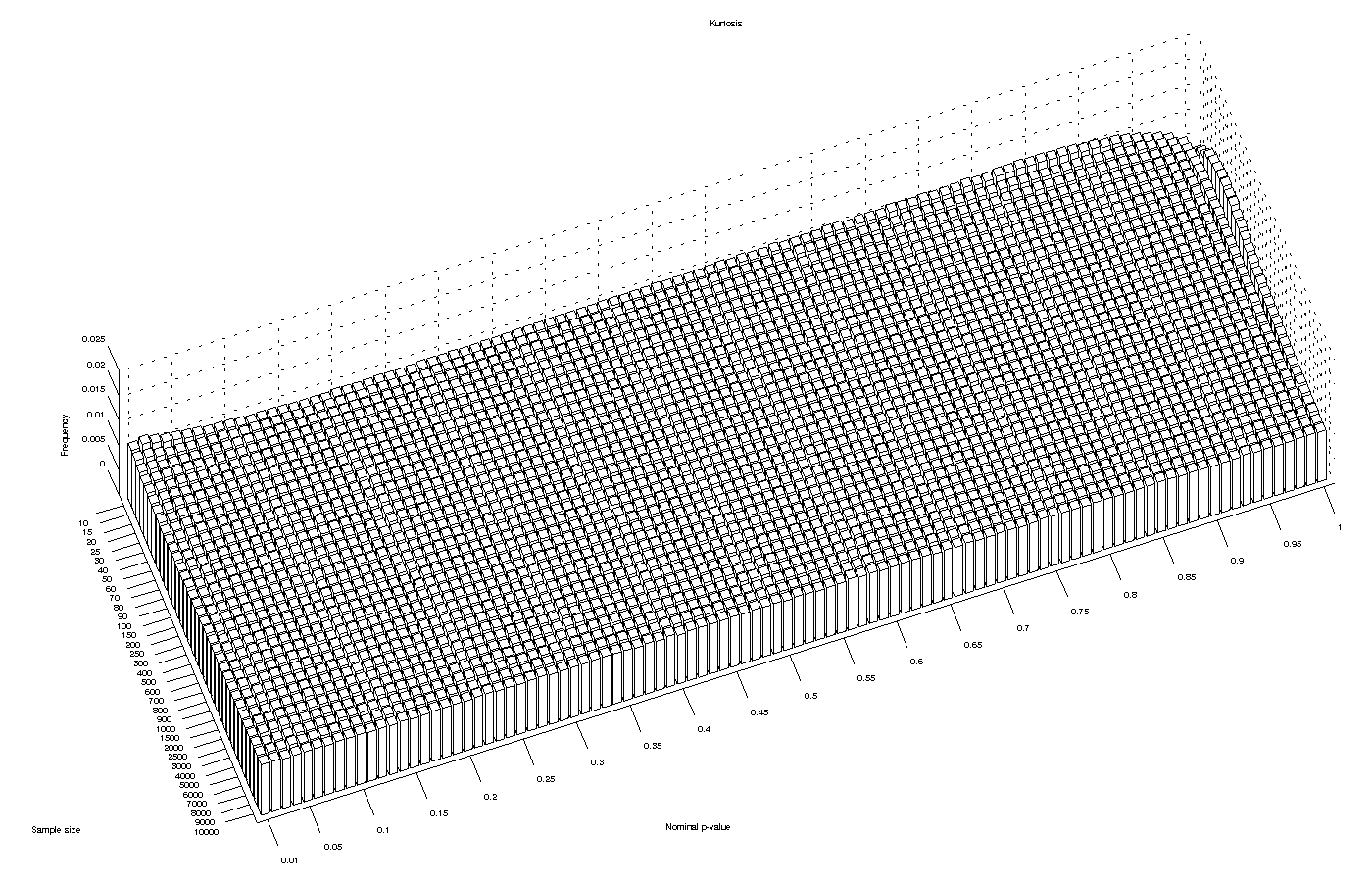
Kurtosis test

The asymptotic approximation for the kurtosis test performed reasonably well for most significance levels and for large sample sizes. However, it produced an excess of low p-values for sample sizes smaller than 20, implying that the test can be anti-conservative with small samples.

D’Agostino-Pearson omnibus test

The p-value approximation for the D’Agostino-Pearson $K^2$ statistic had a poor and erratic behaviour for sample sizes smaller than 200, particularly at the low significance levels, which are generally the ones of greatest interest. For this test, Monte Carlo simulations to derive the critical values are highly recommended.

Jarque-Bera test

Another test for which the asymptotic approximation was poor is the Jarque-Bera test. The approximation to the distribution of the $\text{LM}$ statistic is not valid for small p-values for any of the sample sizes tested, although for sample sizes >1500 the behaviour was reasonably stable. Monte Carlo simulations also more appropriate for this test.

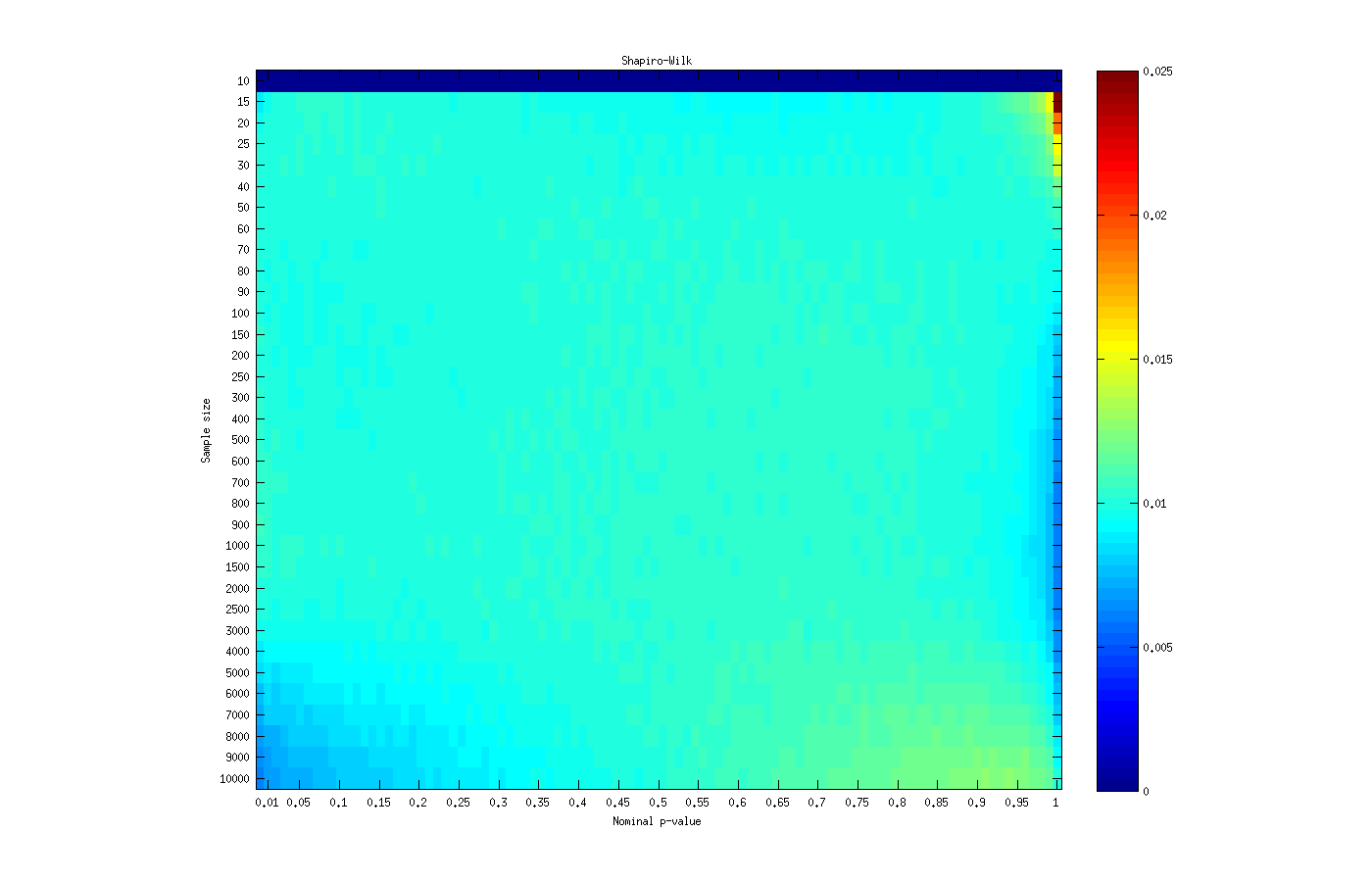
Shapiro-Wilk test

The asymptotic approximation to the distribution of the Shapiro-Wilk’s $W$ statistic seems adequate for sample sizes larger than 15 and smaller than 4000, being slightly anticonservative for most p-values at sample sizes smaller than 20. It has aberrant behaviour at p-values close to 1, which are generally of no interest anyway.

Shapiro-Francia test

For the Shapiro-Francia’s $W'$ statistic, the asymptotic behaviour is similar to the observed for the Shapiro-Wilk test, except that it remains valid for sample sizes larger than 4000.

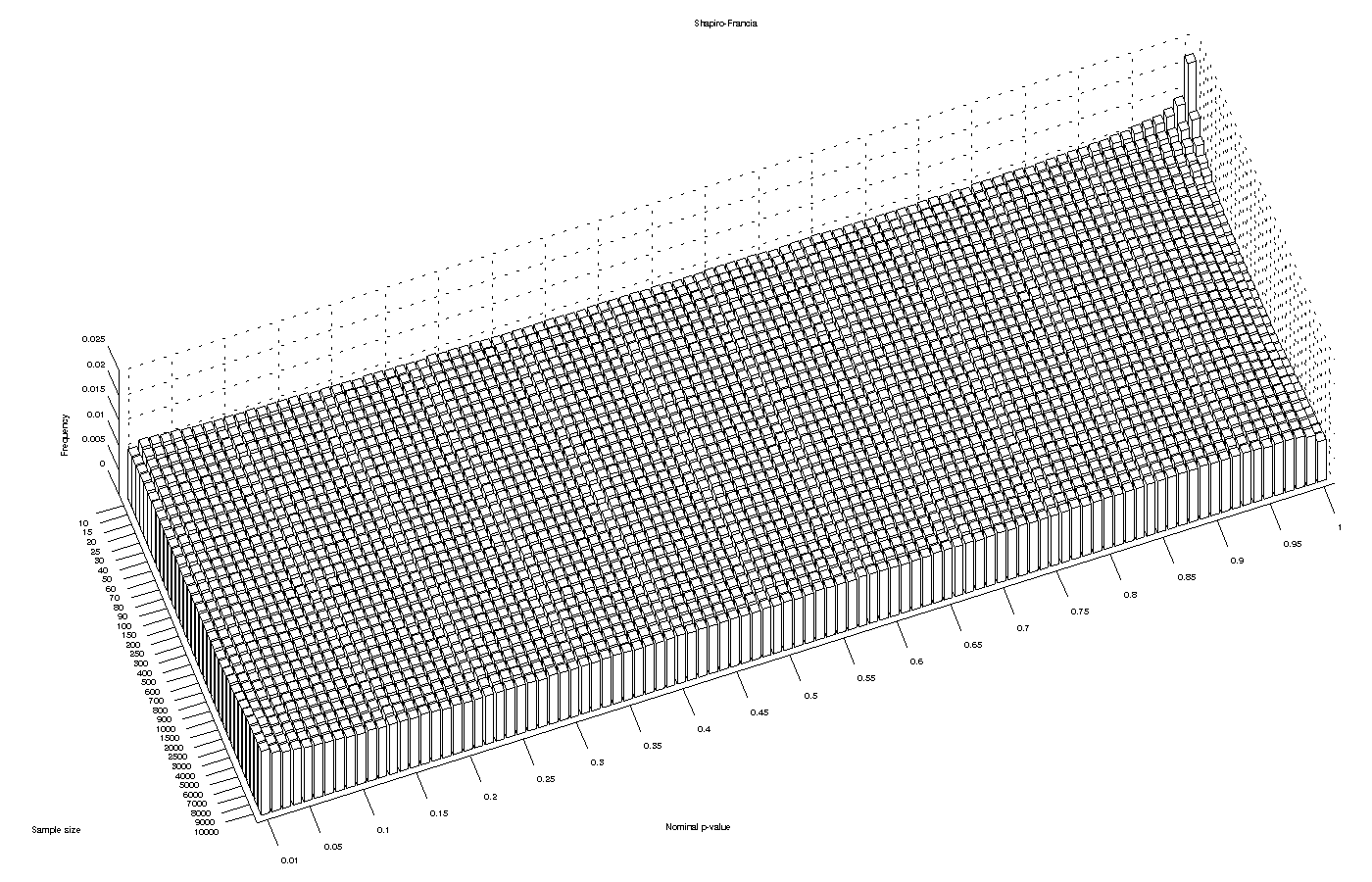
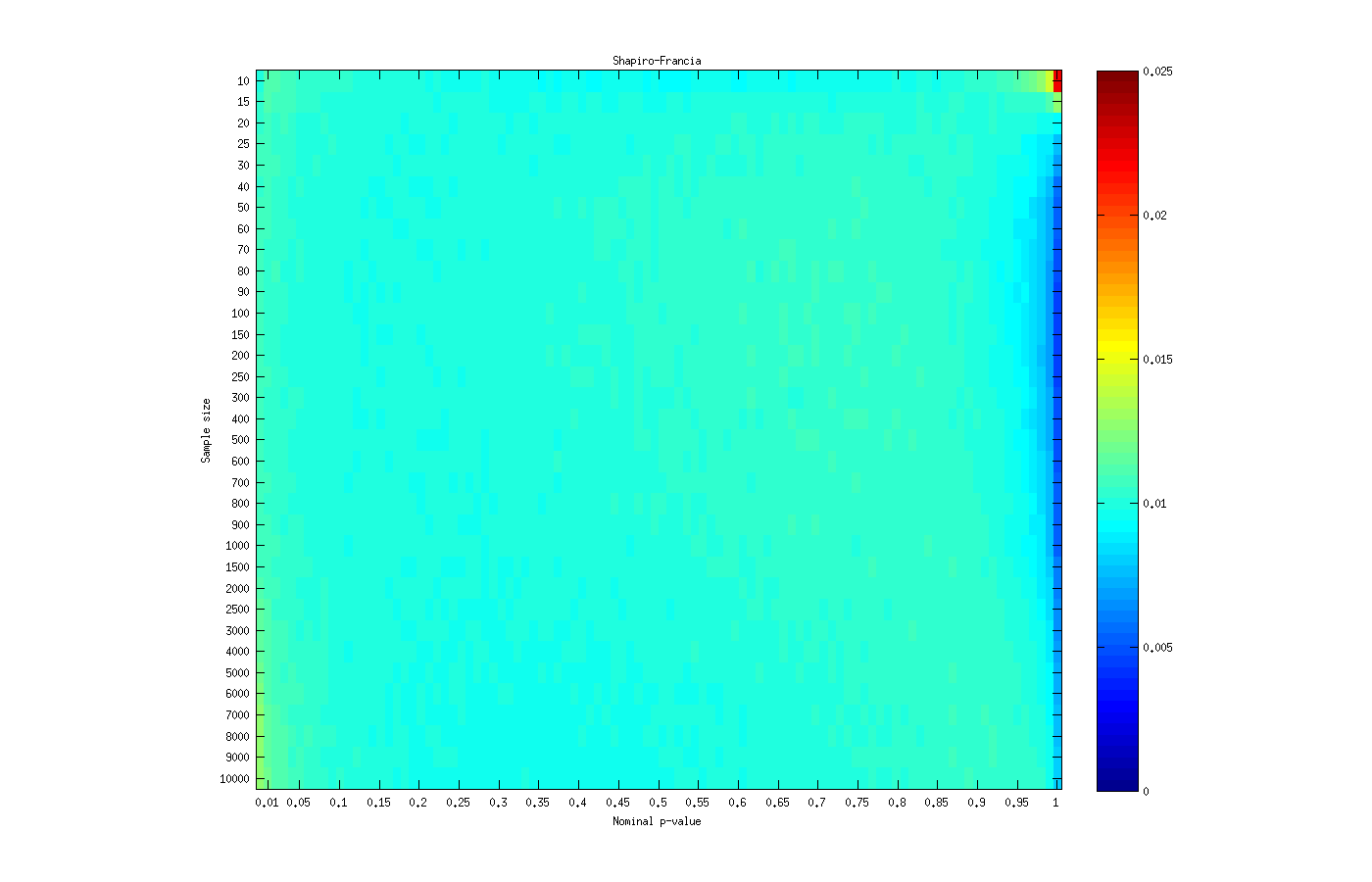
Other tests

Other popular normality or distributional tests, such as the Kolmogorov-Smirnov test, the Lilliefors test, the Cramér-von Mises criterion or the Anderson-Darling test, do not have well established asymptotic approximations and, as a consequence, depend on Monte Carlo simulations to derive critical values. The p-values for these tests are always accurate, as long as the simulations were performed adequately.

Conclusion

Care should be taken when using formulas that approximate the distribution for the statistic for these tests. The approximations are not perfectly valid for all sample sizes, and can be very inaccurate in many cases. When in doubt, critical values based on Monte Carlo tests might be preferred.

FreeSurfer brains in arbitrary colours

Posted on 05.July.2011 by A. M. Winkler

Suppose you run a statistical test for each of the regions of the parcellated brain produced by FreeSurfer. It can be either surface area comparison between groups, or maybe differences in thickness. For each region, you may obtain a statistical score and likely a p-value as well. How to display these results in a color-coded brain model, still inside FreeSurfer?

The process is consists of three steps:

Create of a table with your results, in a format that FreeSurfer can read.
Embed the table in an annotation file.
Display in tksurfer.

1. Create a table

The table must contain not the actual scalars, but instead rgb triplets. This can be done using a simple Octave or matlab script. Since often these results are tabulated as spreadsheets, an alternative, straightforward way is using software like LibreOffice, which gives instantaneous graphical feedback of how the resulting table looks like.

An example of such a spreadsheet is this: colormap.ods. The data go into the sheets named lh.data and rh.data. For structures that are not supposed to display any color, put an off-range value below the minimum value of the other regions (e.g. -1 if the scalars are all positive). Do not add or remove structures.

The sheet named colormap contains the key between the scalar values and the actual rgb colors. In this sheet, the first column (column A) is simply a rank number, used in the calculations; the second column (col. B) contains the range of values between 0 and max, regularly spaced. The remaining three columns (C, D and E) contains the rgb triplets to be assigned to each value in column B. For each scalar to be shown, the closest number has its corresponding rgb used.

The sheets named lh.aparc.annot.ctab and rh.aparc.annot.ctab contain the resulting tables that will be used for actual display purposes. Each contain an index number, starting from 0, the structure name as used in FreeSurfer, the rgb colors, and a fourth value that is called “flag” and is usually zero.

In most cases, only the numerical values in lh.data and rh.data have to be changed. In some occasions, it may be necessary to change the range to be shown (i.e., column B on the colormap sheet), or the colormap itself (columns C, D and E). Different colormaps can be generated, for instance, using Octave. In the file used here, the colormap is the “spectrum”, also known as “jet”, shown below:

Finally, FreeSurfer cannot read binary spreadsheets like this. The file has to be converted to simple values separated by space. In LibreOffice or OpenOffice, there is a very simple way of doing this. Go to File -> Save As… In the File type, choose Text CSV, and make sure to mark the option Edit Filter Settings:

On the next window, as Field Delimiter, choose {space}. As Text delimiter, leave blank, as shown below:

The resulting file, saved to the disk, should look like this (click here for the full file):
0 bankssts 92 255 163 0 1 caudalanteriorcingulate 143 255 112 0 2 caudalmiddlefrontal 0 92 255 0 [...] 34 transversetemporal 255 133 0 0 35 unknown 160 160 160 0

2. Embed the table into annotation file

Once a table has been produced, it can be embedded into the annotation file that defines the the vertices that belong to each region. The annotation files produced by FreeSurfer already contain a default color table, which can be replaced. This can be accomplished by the Octave function replace_ctab.m. This function needs Octave 3.4.0+ or matlab. Type help replace_ctab at the prompt to get usage information. Here is an example:

replace_ctab('${SUBJECTS_DIR}/bert/label/lh.aparc.annot',...
'${SUBJECTS_DIR}/bert/label/lh.aparc.annot.ctab.csv',...
'${SUBJECTS_DIR}/bert/label/lh.aparc.annot.new');

In this example, the original annotation is stored in the file ${SUBJECTS_DIR}/bert/label/lh.aparc.annot, the new color table, as saved in LibreOffice, is in the file ${SUBJECTS_DIR}/bert/label/lh.aparc.annot.ctab. The new annotation file, with the new colortable, will be in the file ${SUBJECTS_DIR}/bert/label/lh.aparc.annot.new. Notice that for the function replace_ctab to work, the directory ${FREESURFER_HOME}/matlab must be in the Octave or matlab path.

3. Display with tksurfer

Once the new annotation file has been produced, display the result is straightforward:

tksurfer bert lh pial -annotation lh.aparc.annot.new

The result should be like the brain shown at the beginning of this article.

Update (01.Aug.2013): In more recent FS versions, the “lh” in front of the annotation file can be omitted, as it’s already specified in the same command line (thanks to Krishna Pancholi, Olin Neuropsychiatric Research Center, for the tip.). This affects only the last command line, which becomes then:

tksurfer bert lh pial -annotation aparc.annot.new

Normality tests I: Brief overview

Posted on 03.July.2011 by A. M. Winkler

Before the fast computers era, it was difficult to test how valid certain statistical methods were. Even in the 1970’s and 1980’s, when computers were already available at Universities and even at home, certain matrix operations were limited by hardware constraints. We are now at a much more comfortable position to analyse how these methods perform. One area where (nowadays) simple computer runs can be illuminating is with respect to normality tests. Tests to evaluate normality or a specific distribution, frequentist approaches can be broadly divided into two categories:

Tests based on comparison (“best fit”) with a given distribution, often specified in terms of its cumulative distribution funtion (cdf). Examples are the Kolmogorov-Smirnov test, the Lilliefors test, the Anderson-Darling test, the Cramér-von Mises criterion, as well as the Shapiro-Wilk and Shapiro-Francia tests.
Tests based on descriptive statistics of the sample. Examples are the skewness test, the kurtosis test, the D’Agostino-Pearson omnibus test, the Jarque-Bera test.

In this article I’ll briefly review six well-known normality tests: (1) the test based on skewness, (2) the test based on kurtosis, (3) the D’Agostino-Pearson omnibus test, (4) the Shapiro-Wilk test, (5) the Shapiro-Francia test, and (6) the Jarque-Bera test. In a subsequent article, I’ll analyse the analytical p-value approximations for these tests, and in a third article, I’ll provide Monte Carlo critical values for each of them.

Skewness test

The skewness of the sample data can be converted to an useful score to evaluate normality with the following transformation (D’Agostino, 1970):

Compute the sample skewness $\sqrt{b_1} = m_3/m_2^{3/2}$ , where $m_k=\sum_i (X_i-\bar X)^k/n$ is the k-th moment, $\bar X=\sum_i X_i/n$ is the sample mean, and $n$ is the sample size.
Compute:
$Y = \sqrt{b_1}\left(\frac{(n+1)(n+3)}{6(n+2)}\right)^{1/2}$
$\beta_2(\sqrt{b_1}) = \frac{3(n^2+27n-70)(n+1)(n+3)}{(n-2)(n+5)(n+7)(n+9)}$
$W^2 = -1+(2(\beta_2(\sqrt{b_1})-1))^{1/2}$
$\delta = 1/\sqrt{\ln W}$
$\alpha = (2/(W^2-1))^{1/2}$
Compute:
$Z(\sqrt{b_1}) = \delta \ln(Y/\alpha + ((Y/\alpha)^2+1)^{1/2})$

The $Z(\sqrt{b_1})$ is the test statistic and it is approximately normally distributed under the null hypothesis that the population data follows a normal distribution.

Kurtosis test

Like the test based on skewness, the test based on kurtosis needs that the sample kurtosis is calculated, then transformed, and finally converted to a p-value. The steps are (Anscombe & Glynn, 1983):

Compute the sample kurtosis $b_2=m_4/m_2^2$ , where $m_k=\sum_i (X_i-\bar X)^k/n$ is the k-th moment, $\bar X=\sum_i X_i/n$ is the sample mean, and $n$ is the sample size.
Compute:
$\mathsf{E}\{b_2\} = 3(n-1)/(n+1)$
$\mathsf{var}\{b_2\} = \frac{24n(n-2)(n-3)}{(n+1)^2(n+3)(n+5)}$
$x = (b_2-\mathsf{E}\{b_2\})/\sqrt{\mathsf{var}\{b_2\}}$
$\sqrt{\beta_1(b_2)}=\frac{6(n^2-5n+2)}{(n+7)(n+9)}\sqrt{\frac{6(n+3)(n+5)}{n(n-2)(n-3)}}$
$A = 6+\frac{8}{\sqrt{\beta_1(b_2)}}\left(\frac{2}{\sqrt{\beta_1(b_2)}}+\sqrt{1+\frac{4}{\beta_1(b_2)}}\right)$ , where $\mathsf{E}\{\cdot\}$ and $\mathsf{var}\{\cdot\}$ represent respectively the expected value and the variance.
Compute:
$Z(b_2) = \left(\left(1-\frac{2}{9A}\right)-\left(\frac{1-2/A}{1+x\sqrt{2/(A-4)}}\right)^{1/3}\right)/\sqrt{\frac{2}{9A}}$

The $Z(b_2)$ is the test statistic and is considered approximately normally distributed under the null hypothesis that the population data follows a normal distribution.

D’Agostino-Pearson omnibus test

The skewness and kurtosis tests can be combined to produce a single, global, “omnibus” statistic. This global test has been proposed by D’Agostino and Pearson (1973) and its statistic is simply $K^2=(Z(\sqrt{b_1}))^2 + (Z(b_2))^2$ . In other words, simply square the statistics from the skewness and kurtosis tests and sum them together. The distribution of the $K^2$ statistic is approximately a $\chi^2$ distribution with two degrees of freedom under the null hypothesis that the sample was drawn from a population with normally distributed values. The skewness, kurtosis and the D’Agostino-Pearson tests have been collectively reviewed and discussed in D’Agostino et al. (1990).

A matlab/Octave implementation of the D’Agostino-Pearson test is available here: daptest.m.

Jarque-Bera test

In a certain regard, this test, introduced by Jarque & Bera (1980) and later discussed in more detail in Jarque & Bera (1987), could also be called an “omnibus” test, that combines skewness and kurtosis into a single statistic. The test statistic is given by $\text{\textsc{lm}}= n\left(\frac{(\sqrt{b_1})^2}{6} + \frac{(b_2-3)^2}{24}\right)$ . The $\text{\textsc{lm}}$ is asymptotically distributed as a $\chi^2$ distribution with two degrees of freedom under the null hypothesis that the sample was drawn from a population with normally distributed values.

A matlab/Octave implementation of the Jarque-Bera test is available here: jbtest.m.

Shapiro-Wilk test

The Shapiro & Wilk (1965) test depends on the covariance matrix between the order statistics of the observations. Values for this covariance matrix have been laboriously tabulated for small samples (Sahan & Greenberg,1956) and algorithms have been developed (Davis & Stephens, 1978; Royston, 1982). In an effort to produce equivalents, yet computationally affordable results, it has been suggested to use approximations. The description here follow the approximation suggested by Royston (1992).

Sort the data in ascending order.
Compute the sample mean $\bar X=\sum_i X_i/n$ , where $n$ is the sample size.
Compute the Blom scores (Blom, 1958) as $\tilde m_i = \Phi^{-1}\{(i-3/8)/(n+1/4)\}$ , where $i$ is the rank order and $\Phi^{-1}\{\cdot\}$ represents the inverse normal cdf.
Compute a set of weights $c_i = \tilde m_i \sqrt{(\mathbf{\tilde m}'\mathbf{\tilde m})}$ . These weights are the same used in the Shapiro-Francia test (see below).
Compute $\tilde a_n= - 2.706056u^5 + 4.434685u^4 - 2.071190u^3 - 0.147981u^2 + 0.221157u + c_n$ , where $u=n^{-1/2}$ . If $n>5$ , compute also $\tilde a_{n-1}= -3.582633u^4 + 5.682633u^4 -1.752461u^3 -0.293762u^2 + 0.042981u + c_{n-1}$ .
Compute $\phi = (\mathbf{\tilde m}'\mathbf{\tilde m} - 2\tilde m_n^2)/(1-2\tilde a_n^2)$ if $n \leq 5$ or $\phi = (\mathbf{\tilde m}'\mathbf{\tilde m} - 2\tilde m_n^2 - 2\tilde m_{n-1}^2)/(1-2\tilde a_n^2-2\tilde a_{n-1}^2)$ otherwise.
Compute the remaining $\tilde a_i = \phi^{-1/2} \tilde m_i$ for $i=2, \ldots ,n-1$ if $n \leq 5$ or $i=3,\ldots ,n-2$ if $n>5$ .
Compute the test statistic $W=\left(\sum_i \tilde a_i X_i \right)^2 / \sum_i (X_i-\bar X)^2$ .

Once the test statistic $W$ has been produced, it can be approximated through a function $g(W)$ to a normal distribution with mean $\mu$ and standard deviation $\sigma$ (Royston, 1993). For sample sizes between 4 and 11 (inclusive), $g(W)=-\ln(\gamma-\ln(1-W))$ , where $\gamma=0.459n-2.273$ . For sample sizes equal to or larger than 12, $g(W)=\ln(1-W)$ .

For $4 \leq n \leq 11$ , the parameters of the statistic transformed (normalized) by $g(W)$ are given by $\mu=-0.0006714n^3 + 0.025054n^2 -0.39978n + 0.5440$ and $\sigma=\mathsf{exp}\{-0.0020322n^3+ 0.062767n^2 -0.77857n + 1.3822\}$ . For $n \geq 12$ , $\mu = 0.0038915u^3 -0.083751u^2 -0.31082u -1.5851$ and $\sigma = \mathsf{exp}\{0.0030302u^2 -0.082676u -0.4803\}$ , where $u = \ln(n)$ .

A $Z$ statistic can then be produced trivially by $(g(W)-\mu)/\sigma$ , and the p-values can be obtained from the normal cdf.

A matlab/Octave implementation of the Shapiro-Wilk test is available here: swtest.m.

Shapiro-Francia test

The test was proposed by Shapiro & Francia (1972) as a simplification of the Shapiro-Wilk test. The simplification consisted in replacing the covariance matrix of the order statistics by the identity matrix. The test is generally considered asymptotically equivalent to the Shapiro-Wilk test for large and independent samples. To apply the test, the steps are (Royston, 1993):

Sort the data in ascending order.
Compute the sample mean $\bar X=\sum_i X_i/n$ , where $n$ is the sample size.
Compute the Blom scores (Blom, 1958) as $\tilde m_i = \Phi^{-1}\{(i-3/8)/(n+1/4)\}$ , where $i$ is the rank order and $\Phi^{-1}\{\cdot\}$ represents the inverse normal cumulative distribution function (cdf).
Compute a set of weights $c_i = \tilde m_i \sqrt{(\mathbf{\tilde m}'\mathbf{\tilde m})}$ .
Compute the test statistic $W'=\left(\sum_i c_i X_i \right)^2 / \sum_i (X_i-\bar X)^2$ .

Similarly as for the Shapiro-Wilk test, once the test statistic $W'$ has been produced, it can be approximated through a function $g(W')=\ln(1-W')$ to a normal distribution with mean $\mu$ and standard deviation $\sigma$ (Royston, 1993). The parameters of the statistic transformed (normalized) by $g(W')$ are given by $\mu=1.0521u - 1.2725$ , where $u = \ln(\ln(n))-\ln(n)$ and $\sigma=-0.26758v+1.030$ , where $v = \ln(\ln(n))+2/\ln(n)$ . These approximations are valid for samples between 5 and 5000 at least.