(This article is about the nifti-1 file format. For an overview of how the nifti-2 differs from the nifti-1, see this one.)
The Neuroimaging Informatics Technology Initiative (nifti) file format was envisioned about a decade ago as a replacement to the then widespread, yet problematic, analyze 7.5 file format. The main problem with the previous format was perhaps the lack of adequate information about orientation in space, such that the stored data could not be unambiguously interpreted. Although the file was used by many different imaging software, the lack of adequate information on orientation obliged some, most notably spm, to include, for every analyze file, an accompanying file describing the orientation, such as a file with extension .mat. The new format was defined in two meetings of the so called Data Format Working Group (dfwg) at the National Institutes of Health (nih), one in 31 March and another in 02 September of 2003. Representatives of some of the most popular neuroimaging software agreed upon a format that would include new information, and upon using the new format, either natively, or have it as an option to import and export.
Radiological or “neurological”?
Perhaps the most visible consequence of the lack of orientation information was the then reigning confusion between left and right sides of brain images during the years in which the analyze format was dominant. It was by this time that researchers became used to describe an image as being in “neurological” or in “radiological” convention. These terms have always been inadequate because, in the absence of orientation information, no two pieces of software necessarily would have to display the same file with the same side of the brain in the same side of the screen. A file could be shown in “neurological” orientation in one software, but in radiological orientation in another, to the dismay of an unaware user. Moreover, although there is indeed a convention adopted by virtually all manufacturers of radiological equipment to show the left side of the patient on the right side of the observer, as if the patient were being observed from face-to-face or, if lying supine, from the feet, it is not known whether reputable neurologists ever actually convened to create a “neurological” convention that would be just the opposite of the radiological. The way as radiological exams are normally shown reflects the reality of the medical examination, in which the physician commonly approaches the patient in the bed from the direction of the feet (usually there is a wall behind the bed), and tend to stay face-to-face most of the time. Although the neurological examination does indeed include a few manoeuvres performed at the back, for most of the time, even in the more specialised semiotics, the physician stays at the front. The nifti format obviated all these issues, rendering these terms obsolete. Software can now mark the left or the right side correctly, sometimes giving the option of showing it flipped to better adapt to the user personal orientation preference.
Same format, different presentations
A single image stored in the analyze 7.5 format requires two files: a header, with extension .hdr, to store meta-information, and the actual data, with extension .img. In order to keep compatibility with the previous format, data stored in nifti format also uses a pair of files, .hdr/.img. Care was taken so that the internal structure of the nifti format would be mostly compatible with the structure of the analyze format. However, the new format added some clever improvements. Work with a pair of files for each image as in the .hdr/.img, rather than just one, is not only inconvenient, but it is also error prone, as one might easily forget (or not know) that the data of interest is actually split across more than one file. To address this issue, the nifti format also allows for storage as a single file, with extension .nii. Single file or pair of files are not the only possible presentations, though. It is very common for images to have large areas of solid background, or files describing masks and regions of interest containing just a few unique values that appear repeated many times. Files like these occupy large space in the disk, but with little actual information content. This is the perfect case where compression can achieve excellent results. Indeed, both nifti and analyze files can be compressed. The deflate algorithm (used, e.g., by gzip) can operate in streams, allowing compression and decompression on-the-fly. The compressed versions have the .gz extension appended: .nii.gz (single file) or .hdr/.img.gz (pair of files, either nifti or analyze).
Predefined dimensions for space and time
In the nifti format, the first three dimensions are reserved to define the three spatial dimensions — x, y and z —, while the fourth dimension is reserved to define the time points — t. The remaining dimensions, from fifth to seventh, are for other uses. The fifth dimension, however, can still have some predefined uses, such as to store voxel-specific distributional parameters or to hold vector-based data.
Overview of the header structure
In order to keep compatibility with the analyze format, the size of the nifti header was maintained at 348 bytes as in the old format. Some fields were reused, some were preserved, but ignored, and some were entirely overwritten. The table below shows each of the fields, their sizes, and a brief description. More details on how each field should be interpreted are provided further below.
| Type |
Name |
Offset |
Size |
Description |
int |
sizeof_hdr |
0B |
4B |
Size of the header. Must be 348 (bytes). |
char |
data_type[10] |
4B |
10B |
Not used; compatibility with analyze. |
char |
db_name[18] |
14B |
18B |
Not used; compatibility with analyze. |
int |
extents |
32B |
4B |
Not used; compatibility with analyze. |
short |
session_error |
36B |
2B |
Not used; compatibility with analyze. |
char |
regular |
38B |
1B |
Not used; compatibility with analyze. |
char |
dim_info |
39B |
1B |
Encoding directions (phase, frequency, slice). |
short |
dim[8] |
40B |
16B |
Data array dimensions. |
float |
intent_p1 |
56B |
4B |
1st intent parameter. |
float |
intent_p2 |
60B |
4B |
2nd intent parameter. |
float |
intent_p3 |
64B |
4B |
3rd intent parameter. |
short |
intent_code |
68B |
2B |
nifti intent. |
short |
datatype |
70B |
2B |
Data type. |
short |
bitpix |
72B |
2B |
Number of bits per voxel. |
short |
slice_start |
74B |
2B |
First slice index. |
float |
pixdim[8] |
76B |
32B |
Grid spacings (unit per dimension). |
float |
vox_offset |
108B |
4B |
Offset into a .nii file. |
float |
scl_slope |
112B |
4B |
Data scaling, slope. |
float |
scl_inter |
116B |
4B |
Data scaling, offset. |
short |
slice_end |
120B |
2B |
Last slice index. |
char |
slice_code |
122B |
1B |
Slice timing order. |
char |
xyzt_units |
123B |
1B |
Units of pixdim[1..4]. |
float |
cal_max |
124B |
4B |
Maximum display intensity. |
float |
cal_min |
128B |
4B |
Minimum display intensity. |
float |
slice_duration |
132B |
4B |
Time for one slice. |
float |
toffset |
136B |
4B |
Time axis shift. |
int |
glmax |
140B |
4B |
Not used; compatibility with analyze. |
int |
glmin |
144B |
4B |
Not used; compatibility with analyze. |
char |
descrip[80] |
148B |
80B |
Any text. |
char |
aux_file[24] |
228B |
24B |
Auxiliary filename. |
short |
qform_code |
252B |
2B |
Use the quaternion fields. |
short |
sform_code |
254B |
2B |
Use of the affine fields. |
float |
quatern_b |
256B |
4B |
Quaternion b parameter. |
float |
quatern_c |
260B |
4B |
Quaternion c parameter. |
float |
quatern_d |
264B |
4B |
Quaternion d parameter. |
float |
qoffset_x |
268B |
4B |
Quaternion x shift. |
float |
qoffset_y |
272B |
4B |
Quaternion y shift. |
float |
qoffset_z |
276B |
4B |
Quaternion z shift. |
float |
srow_x[4] |
280B |
16B |
1st row affine transform |
float |
srow_y[4] |
296B |
16B |
2nd row affine transform. |
float |
srow_z[4] |
312B |
16B |
3rd row affine transform. |
char |
intent_name[16] |
328B |
16B |
Name or meaning of the data. |
char |
magic[4] |
344B |
4B |
Magic string. |
| Total size |
348B |
|
Each of these fields is described in mode detail below, in the order as they appear in the header.
Size of the header
The field int sizeof_hdr stores the size of the header. It must be 348 for a nifti or analyze format.
Dim info
The field char dim_info stores, in just one byte, the frequency encoding direction (1, 2 or 3), the phase encoding direction (1, 2 or 3), and the direction in which the volume was sliced during the acquisition (1, 2 or 3). For spiral sequences, frequency and phase encoding are both set as 0. The reason to collapse all this information in just one byte was to save space. See also the fields short slice_start, short slice_end, char slice_code and float slice_duration.
Image dimensions
The field short dim[8] contains the size of the image array. The first element (dim[0]) contains the number of dimensions (1-7). If dim[0] is not in this interval, the data is assumed to have opposite endianness and so, should be byte-swapped (the nifti standard does not specify a specific field for endianness, but encourages the use of dim[0] for this purpose). The dimensions 1, 2 and 3 are assumed to refer to space (x, y, z), the 4th dimension is assumed to refer to time, and the remaining dimensions, 5, 6 and 7, can be anything else. The value dim[i] is a positive integer representing the length of the i-th dimension.
Intent
The short intent_code is an integer that codifies that the data is supposed to contain. Some of these codes require extra-parameters, such as the number of degrees of freedom (df). These extra parameters, when needed, can be stored in the fields intent_p* when they can be applied to the image as a while, or in the 5th dimension if voxelwise. A list of intent codes is in the table below:
| Intent |
Code |
Parameters |
| None |
0 |
no parameters |
| Correlation |
2 |
p1 = degrees of freedom (df) |
| t test |
3 |
p1 = df |
| F test |
4 |
p1 = numerator df, p2 = denominator df |
| z score |
5 |
no parameters |
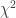 statistic statistic |
6 |
p1 = df |
| Beta distribution |
7 |
p1 = a, p2 = b |
| Binomial distribution |
8 |
p1 = number of trials, p2 = probability per trial |
| Gamma distribution |
9 |
p1 = shape, p2 = scale |
| Poisson distribution |
10 |
p1 = mean |
| Normal distribution |
11 |
p1 = mean, p2 = standard deviation |
| Noncentral F statistic |
12 |
p1 = numerator df, p2 = denominator df, p3 = numerator noncentrality parameter |
Noncentral 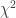 statistic statistic |
13 |
p1 = dof, p2 = noncentrality parameter |
| Logistic distribution |
14 |
p1 = location, p2 = scale |
| Laplace distribution |
15 |
p1 = location, p2 = scale |
| Uniform distribution |
16 |
p1 = lower end, p2 = upper end |
| Noncentral t statistic |
17 |
p1 = dof, p2 = noncentrality parameter |
| Weibull distribution |
18 |
p1 = location, p2 = scale, p3 = power |
 distribution distribution |
19 |
p1 = df* |
| Inverse Gaussian |
20 |
p1 =  , p2 = , p2 =  |
| Extreme value type I |
21 |
p1 = location, p2 = scale |
| p-value |
22 |
no parameters |
| -ln(p) |
23 |
no parameters |
| -log(p) |
24 |
no parameters |
* Note: For the  distribution, when p1=1, it is a “half-normal” distribution; when p1=2, it is a Rayleigh distribution; and when p1=3, it is a Maxwell-Boltzmann distribution. Other intent codes are available to indicate that the file contains data that is not of statistical nature.
distribution, when p1=1, it is a “half-normal” distribution; when p1=2, it is a Rayleigh distribution; and when p1=3, it is a Maxwell-Boltzmann distribution. Other intent codes are available to indicate that the file contains data that is not of statistical nature.
| Intent |
Code |
Description |
| Estimate |
1001 |
Estimate of some parameter, possibly indicated in intent_name |
| Label |
1002 |
Indices of a set of labels, which may be indicated in aux_file. |
| NeuroName |
1003 |
Indices in the NeuroNames set of labels. |
| Generic matrix |
1004 |
For a MxN matrix in the 5th dimension, row major. p1 = M, p2 = N (integers as float); dim[5] = M*N. |
| Symmetric matrix |
1005 |
For a symmetric NxN matrix in the 5th dimension, row major, lower matrix. p1 = N (integer as float); dim[5] = N*(N+1)/2. |
| Displacement vector |
1006 |
Vector per voxel, stored in the 5th dimension. |
| Vector |
1007 |
As above, vector per voxel, stored in the 5th dimension. |
| Point set |
1008 |
Points in the space, in the 5th dimension. dim[1] = number of points; dim[2]=dim[3]=1; intent_name may be used to indicate modality. |
| Triangle |
1009 |
Indices of points in space, in the 5th dimension. dim[1] = number of triangles. |
| Quaternion |
1010 |
Quaternion in the 5th dimension. |
| Dimless |
1011 |
Nothing. The intent may be in intent_name. |
| Time series |
2001 |
Each voxel contains a time series. |
| Node index |
2002 |
Each voxel is an index of a surface dataset. |
| rgb |
2003 |
rgb triplet in the 5th dimension. dim[0] = 5, dim[1] has the number of entries, dim[2:4] = 1, dim[5] = 3. |
| rgba |
2004 |
rgba quadruplet in the 5th dimension. dim[0] = 5, dim[1] has the number of entries, dim[2:4] = 1, dim[5] = 4. |
| Shape |
2005 |
Value at each location is a shape parameter, such as a curvature. |
The intent parameters are stored in the fields float intent_p1, float intent_p2 and float intent_p3. Alternatively, if the parameters are different for each voxel, they should be stored in the 5th dimension of the file. A human readable intent name can be stored in the field char intent_name[16], which may help to explain the intention of the data when it cannot or is not coded with any of the intent codes and parameters above.
Data type and bits per pixel/voxel
The field int datatype indicates the type of the data stored. Acceptable values are:
| Type |
Bitpix |
Code |
| unknown |
– |
0 |
| bool |
1 bit |
1 |
| unsigned char |
8 bits |
2 |
| signed short |
16 bits |
4 |
| signed int |
32 bits |
8 |
| float |
32 bits |
16 |
| complex |
64 bits |
32 |
| double |
64 bits |
64 |
| rgb |
24 bits |
128 |
| “all” |
– |
255 |
| signed char |
8 bits |
256 |
| unsigned short |
16 bits |
512 |
| unsigned int |
32 bits |
768 |
| long long |
64 bits |
1024 |
| unsigned long long |
64 bits |
1280 |
| long double |
128 bits |
1536 |
| double pair |
128 bits |
1792 |
| long double pair |
256 bits |
2048 |
| rgba |
32 bits |
2304 |
The field short bitpix holds the information of the number of bits per voxel. The value must match the type determined by datatype as shown above.
Slice acquisition information
The fields fields char slice_code, short slice_start, short slice_end and float slice_duration are useful to store information about the timing of an fMRI acquisition, and need to be used together with the char dim_info, which contains the field slice_dim. If, and only if, the slice_dim is different than zero, slice_code is interpreted as:
| Code |
Interpretation |
0 |
Slice order unknown |
1 |
Sequential, increasing |
2 |
Sequential, decreasing |
3 |
Interleaved, increasing, starting at the 1st mri slice |
4 |
Interleaved, decreasing, starting at the last mri slice |
5 |
Interleaved, increasing, starting at the 2nd mri slice |
6 |
Interleaved, decreasing, starting at one before the last mri slice |
The fields short slice_start and short slice_end inform respectively which are the first the last slices that correspond to the actual mri acquisition. Slices present in the image that are outside this range are treated as padded slices (for instance, containing zeroes). The field float slice_duration indicates the amount of time needed to acquire a single slice. Having this information in a separate field allows to correctly store images of experiments in which slice_duration*dim[slice_dim] is smaller than the value stored in pixdim[4], usually the repetition time (tr).

Slice codes to specify slice acquisition timings. In this example, slice_start = 2 and slice_end = 11, indicating that slices #01 and #12 stored in the file have not been truly acquired with MRI, but instead, were padded to the file. The field slice_duration specifies how long it took to acquire each slice. The dimension that corresponds to the slice acquisition (in this case dim[3], z) is encoded in the field dim_info.
Voxel dimensions
The dimension for each voxel is stored in the field float pixdim[8], and each element match its respective in short dim[8]. The value in float pixdim[0], however, has a special meaning, discussed below; it should always be -1 or 1. The units of measurement for the first 4 dimensions are specified in the field xyzt_units, discussed below.
Voxel offset
The field int vox_offset indicates, for single files (.nii), the byte offset before the imaging data starts. For compatibility with older software, possible values are multiples of 16, and the minimum value is 352 (the smallest multiple of 16 that is larger than 348). For file pairs (.hdr/.img), this should be set as zero if no information other than image data itself is to be stored in the .img (most common), but it can also be larger than zero, allowing for user-defined extra-information to be prepended into the .img, such as a dicom header. In this case, however, the rule of being a multiple of 16 may eventually be violated. This field is of type float (32-bit, ieee-754), allowing integers up to 224 to be specified. The reason for using float rather than what would be the more natural choice, int, is to allow compatibility with the analyze format.
Data scaling
The values stored in each voxel can be linearly scaled to different units. The fields float scl_slope and float scl_inter define a slope and an intercept for a linear function. The data scaling feature allows the storage in a wider range than what would be allowed by the datatype. Yet, it is possible to use scaling within the same datatype. Both scaling fields should be ignored for the storage of rgb data. For complex types, it should be applied to both real and imaginary parts.
Data display
For files that store scalar (non-vector) data, the fields float cal_min and float cal_max determine the intended display range when the image is opened. Voxel values equal or below cal_min should be shown with the smallest colour in the colourscale (typically black in a gray-scale visualisation), and values equal or above cal_max should be shown with the largest colour in the colourscale (typically white).
Measurement units
Both spatial and temporal measurement units, used for the dimensions dim[1] to dim[4] (and, respectively, for pixdim[]), are encoded in the field char xyzt_units. The bits 1-3 are used to store the spatial dimensions, the bits 4-6 are for temporal dimensions, and the bits 6 and 7 are not used. A temporal offset can be specified in the field float toffset. The codes for xyzt_units, in decimal, are:
| Unit |
Code |
| Unknown |
0 |
| Meter (m) |
1 |
| Milimeter (mm) |
2 |
| Micron (µm) |
3 |
| Seconds (s) |
8 |
| Miliseconds (ms) |
16 |
| Microseconds (µs) |
24 |
| Hertz (Hz) |
32 |
| Parts-per-million (ppm) |
40 |
| Radians per second (rad/s) |
48 |
Description
This field, char descrip[80] can contain any text with up to 80 characters. The standard does not specify whether this string needs to be terminated by a null character or not. Presumably, it is up to the application to correctly handle it.
Auxiliary file
A supplementary file, containing extra-information, can be specified in the field char aux_file[24]. This file can, for instance, contain the face indices for meshes which points are stored in the 5th dimension or a look-up-table to display colours.
Orientation information
The most visible improvement of the nifti format over the previous analyze format is the ability to unambiguously store information orientation. The file standard assumes that the voxel coordinates refer to the center of each voxel, rather than at any of its corners. The world coordinate system is assumed to be ras: +x is Right, +y is Anterior and +z is Superior, which is precisely different than the coordinate system used in analyze, which is las. The format provides three different methods to map the voxel coordinates (i,j,k) to the world coordinates (x,y,z). The first method exists only to allow compatibility with the analyze format. The other two methods may coexist, and convey different coordinate systems. These systems are specified in the fields short qform_code and short sform_code, which can assume the values specified in the table:
| Name |
Code |
Description |
| unknown |
0 |
Arbitrary coordinates. Use Method 1. |
| scanner_anat |
1 |
Scanner-based anatomical coordinates. |
| aligned_anat |
2 |
Coordinates aligned to another file, or to the “truth” (with an arbitrary coordinate center). |
| talairach |
3 |
Coordinates aligned to the Talairach space. |
| mni_152 |
4 |
Coordinates aligned to the mni space. |
In principle, the qform_code (Method 2 below) should contain either 0, 1 or 2, whereas the sform_code (Method 3 below) could contain any of the codes shown in the table.
Method 1
The Method 1 is for compatibility with analyze and is not supposed to be used as the main orientation method. The world coordinates are determined simply by scaling by the voxel size:
![\left[ \begin{array}{c} x\\ y\\ z \end{array} \right]= \left[ \begin{array}{c} i\\ j\\ k \end{array} \right]\odot \left[ \begin{array}{c} \mathtt{pixdim[1]}\\ \mathtt{pixdim[2]}\\ \mathtt{pixdim[3]}\\ \end{array} \right]](https://s0.wp.com/latex.php?latex=%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+x%5C%5C+y%5C%5C+z+%5Cend%7Barray%7D+%5Cright%5D%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+i%5C%5C+j%5C%5C+k+%5Cend%7Barray%7D+%5Cright%5D%5Codot+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cmathtt%7Bpixdim%5B1%5D%7D%5C%5C+%5Cmathtt%7Bpixdim%5B2%5D%7D%5C%5C+%5Cmathtt%7Bpixdim%5B3%5D%7D%5C%5C+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=333333&s=0&c=20201002)
where 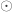 is the Hadamard product.
is the Hadamard product.
Method 2
The Method 2 is used when short qform_code is larger than zero, and is intended to be used to indicate the scanner coordinates, in a way that resembles the coordinates specified in the dicom header. It can also be used to represent the alignment of an image to a previous session of the same subject (such as for coregistration). For compactness and simplicity, the information in this field is stored as quaternions (a,b,c,d), which last three coefficients are in the fields float quatern_b, float quatern_c, float quatern_d. The first coefficient can be calculated from the other three as 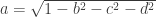 . These fields are used to construct a rotation matrix as:
. These fields are used to construct a rotation matrix as:
![\mathbf{R} = \left[ \begin{array}{ccc} a^2+b^2-c^2-d^2 & 2(bc-ad) & 2(bd+ac) \\ 2(bc+ad) & a^2+c^2-b^2-d^2 & 2(cd-ab) \\ 2(bd-ac) & 2(cd+ab) & a^2+d^2-b^2-c^2 \end{array} \right]](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BR%7D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bccc%7D+a%5E2%2Bb%5E2-c%5E2-d%5E2+%26+2%28bc-ad%29+%26+2%28bd%2Bac%29+%5C%5C+2%28bc%2Bad%29+%26+a%5E2%2Bc%5E2-b%5E2-d%5E2+%26+2%28cd-ab%29+%5C%5C+2%28bd-ac%29+%26+2%28cd%2Bab%29+%26+a%5E2%2Bd%5E2-b%5E2-c%5E2+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=333333&s=0&c=20201002)
This rotation matrix, together with the voxel sizes and a translation vector, is used to define the final transformation from voxel to world space:
![\left[ \begin{array}{c} x\\ y\\ z \end{array} \right]=\mathbf{R} \left[ \begin{array}{c} i\\ j\\ q\cdot k\\ \end{array} \right]\odot \left[ \begin{array}{c} \mathtt{pixdim[1]}\\ \mathtt{pixdim[2]}\\ \mathtt{pixdim[3]}\\ \end{array} \right]+ \left[ \begin{array}{c} \mathtt{qoffset\_x}\\ \mathtt{qoffset\_y}\\ \mathtt{qoffset\_z}\\ \end{array} \right]](https://s0.wp.com/latex.php?latex=%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+x%5C%5C+y%5C%5C+z+%5Cend%7Barray%7D+%5Cright%5D%3D%5Cmathbf%7BR%7D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+i%5C%5C+j%5C%5C+q%5Ccdot+k%5C%5C+%5Cend%7Barray%7D+%5Cright%5D%5Codot+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cmathtt%7Bpixdim%5B1%5D%7D%5C%5C+%5Cmathtt%7Bpixdim%5B2%5D%7D%5C%5C+%5Cmathtt%7Bpixdim%5B3%5D%7D%5C%5C+%5Cend%7Barray%7D+%5Cright%5D%2B+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cmathtt%7Bqoffset%5C_x%7D%5C%5C+%5Cmathtt%7Bqoffset%5C_y%7D%5C%5C+%5Cmathtt%7Bqoffset%5C_z%7D%5C%5C+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=333333&s=0&c=20201002)
where 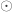 is, again, the Hadamard product, and
is, again, the Hadamard product, and  is the
is the qfac value, stored at the otherwise unused pixdim[0], which should be either -1 or 1. Any different value should be treated as 1.
Method 3
The Method 3 is used when short sform_code is larger than zero. It relies on a full affine matrix, stored in the header in the fields float srow_*[4], to map voxel to world coordinates:
![\left[ \begin{array}{c} x\\ y\\ z\\ 1 \end{array} \right]=\left[ \begin{array}{cccc} \mathtt{srow\_x[0]} & \mathtt{srow\_x[1]} & \mathtt{srow\_x[2]} & \mathtt{srow\_x[3]}\\ \mathtt{srow\_y[0]} & \mathtt{srow\_y[1]} & \mathtt{srow\_y[2]} & \mathtt{srow\_y[3]}\\ \mathtt{srow\_z[0]} & \mathtt{srow\_z[1]} & \mathtt{srow\_z[2]} & \mathtt{srow\_z[3]} \\ 0 & 0 & 0 & 1\end{array} \right]\cdot\left[ \begin{array}{c} i\\ j\\ k\\ 1 \end{array} \right]](https://s0.wp.com/latex.php?latex=%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+x%5C%5C+y%5C%5C+z%5C%5C+1+%5Cend%7Barray%7D+%5Cright%5D%3D%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcccc%7D+%5Cmathtt%7Bsrow%5C_x%5B0%5D%7D+%26+%5Cmathtt%7Bsrow%5C_x%5B1%5D%7D+%26+%5Cmathtt%7Bsrow%5C_x%5B2%5D%7D+%26+%5Cmathtt%7Bsrow%5C_x%5B3%5D%7D%5C%5C+%5Cmathtt%7Bsrow%5C_y%5B0%5D%7D+%26+%5Cmathtt%7Bsrow%5C_y%5B1%5D%7D+%26+%5Cmathtt%7Bsrow%5C_y%5B2%5D%7D+%26+%5Cmathtt%7Bsrow%5C_y%5B3%5D%7D%5C%5C+%5Cmathtt%7Bsrow%5C_z%5B0%5D%7D+%26+%5Cmathtt%7Bsrow%5C_z%5B1%5D%7D+%26+%5Cmathtt%7Bsrow%5C_z%5B2%5D%7D+%26+%5Cmathtt%7Bsrow%5C_z%5B3%5D%7D+%5C%5C+0+%26+0+%26+0+%26+1%5Cend%7Barray%7D+%5Cright%5D%5Ccdot%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+i%5C%5C+j%5C%5C+k%5C%5C+1+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=333333&s=0&c=20201002)
Differently than Method 2, which is supposed to contain a transformation that maps voxel indices to the scanner world coordinates, or to align between two distinct images of the same subject, the Method 3 is used to indicate the transformation to some standard world space, such as the Talairach or mni coordinates, in which case, the coordinate system has its origin (0,0,0) at the anterior comissure of the brain.
Magic string
The char magic[4] field is a “magic” string that declares the file as conforming with the nifti standard. It was placed at the very end of the header to avoid overwriting fields that are needed for the analyze format. Ideally, however, this string should be checked first. It should be 'ni1' (or '6E 69 31 00' in hexadecimal) for .hdr/.img pair, or 'n+1' (or '6E 2B 31 00') for a .nii single file. In the absence of this string, the file should be treated as analyze. Future versions of the nifti format may increment the string to 'n+2', 'n+3', etc. Indeed, as of 2012, a second version is under preparation.
Unused fields
The fields char data_type[10], char db_name[18], int extents, short session_error and char regular are not used by the nifti format, but were included in the header for compatibility with analyze. The extents should be the integer 16384, and regular should be the character 'r'. The fields int glmin and int glmax specify respectively the minimum and maximum of the entire dataset in the analyze format.
Storing extra-information
Extra information can be included in the nifti format in a number of ways as allowed by the standard. At the end of the header, the next 4 bytes (i.e., from byte 349 to 352, inclusive) may or may not be present in a .hdr file. However, these bytes will always be present in a .nii file. They should be interpreted as a character array, i.e. char extension[4]. In principle, these 4 bytes should be all set to zero. If the first, extension[0], is non-zero, this indicates the presence of extended information beginning at the byte number 353. Such extended information needs to have size multiple of 16. The first 8 bytes of this extension should be interpreted as two integers, int esize and int ecode. The field esize indicates the size of the extent, including the first 8 bytes that are the esize and ecode themselves. The field ecode indicates the format used for the remaining of the extension. At the time of this writing, three codes have been defined:
| Code |
Use |
0 |
Unknown. This code should be avoided. |
2 |
dicom extensions |
4 |
xml extensions used by the afni software package. |
More than one extension can be present in the same file, each one always starting with the pair esize and ecode, and with its first byte immediately past the last byte of the previous extension. In a single .nii file, the float vox_offset must be set properly so that the imaging data begins only after the end of the last extension.
Problems
The nifti format brought a number of great benefits if compared to the old analyze format. However, it also brought its own set of new problems. Fortunately, these problems are not severe. Here are some:
- Even though a huge effort was done to keep compatibility with analyze, a crucial aspect was not preserved: the world coordinate system is assumed, in the nifti format, to be ras, which is weird and confusing. The las is a much more logical choice from a medical perspective. Fortunately, since orientation is stored unambiguously, it is possible to later flip the images in the screen at will in most software.
- The file format still relies too much on the file extension being
.nii or on a pair .hdr/.img, rather than much less ambiguous magic strings or numbers. On the other hand, the different magic strings for single file and for file pairs effectively prevent the possibility of file splitting/merging using common operating system tools (such as dd in Linux), as the magic string needs to be changed, even though the header structure remains absolutely identical.
- The magic string that is present in the header is not placed at the beginning, but near its end, which makes the file virtually unrecognisable outside of the neuroimaging field.
- The specification of three different coordinate systems, while bringing flexibility, also brought ambiguity, as nowhere in the standard there is information on which should be preferred when more than one is present. Certain software packages explicitly force the
qform_code and sform_code to be identical to each other.
- There is no field specifying a preferred interpolation method when using Methods 2 or 3, even though these methods do allow fractional voxels to be found with the specification of world coordinates.
- Method 2 allows only rotation and translation, but sometimes, due to all sorts of scanner calibration issues and different kinds of geometric distortion present in different sequences, the coregistration between two images of the same subject may require scaling and shear, which are only provided in Method 3.
- Method 3 is supposed to inform that the data is aligned to a standard space using an affine transformation. This works perfectly if the data has been previously warped to such a space. Otherwise, the simple alignment of any actual brain from native to standard space cannot be obtained with only linear transformations.
- To squeeze information while keeping compatibility with the analyze format, some fields had to be mangled into just one byte, such as
char dim_info and char xyzt_units, which is not practical and require sub-byte manipulation.
- The field
float vox_offset, directly inherited from the analyze format, should in fact, be an integer. Having it as a float only adds confusion.
- Not all software packages implement the format exactly in the same way. Vector-based data, for instance, which should be stored in the 5th dimension, is often stored in the 4th, which should be reserved for time. Although this is not a problem with the format itself, but with the use made of it, easy implementation malpractices lead to a dissemination of ambiguous and ill-formed files that eventually cannot be read in other applications as intended by the time of the file creation.
Despite these issues, the format has been very successful as a means to exchange data between different software packages. An updated format, the nifti 2.0, with a header with more than 500 bytes of information, may become official soon. (UPDATE: details here)
More information
The official definition of the nifti format is available as a c header file (nifti1.h) here and mirrored here.